What Percent Of 84 Is 21
listenit
Apr 03, 2025 · 5 min read
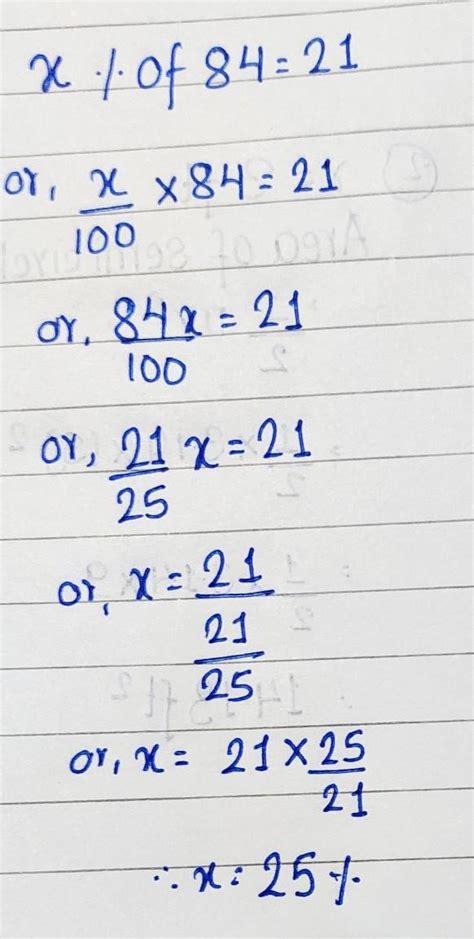
Table of Contents
What Percent of 84 is 21? A Comprehensive Guide to Percentage Calculations
Finding what percentage one number represents of another is a fundamental skill in mathematics with widespread applications in various fields, from everyday budgeting to complex financial analysis. This comprehensive guide will not only answer the question "What percent of 84 is 21?" but also delve into the underlying principles of percentage calculations, exploring different methods and providing practical examples to solidify your understanding.
Understanding Percentages
Before we tackle the specific problem, let's establish a clear understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" signifies "per hundred" or "out of 100." For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Percentages are incredibly useful for representing proportions and comparisons. They provide a standardized way to express ratios, making it easy to understand and interpret data across different contexts. Whether you're calculating discounts, tax rates, or analyzing statistical data, percentages are an essential tool.
Method 1: Using Proportions to Solve "What percent of 84 is 21?"
This method is based on setting up a proportion, equating two ratios. We know that 21 is a part of 84, and we want to find the percentage representing this part. We can set up the proportion as follows:
x/100 = 21/84
Where 'x' represents the percentage we're trying to find. This equation states that the ratio of 'x' to 100 is equal to the ratio of 21 to 84. To solve for 'x', we can cross-multiply:
84x = 21 * 100
84x = 2100
x = 2100 / 84
x = 25
Therefore, 21 is 25% of 84.
Method 2: Using the Formula for Percentage Calculation
Another approach involves using the formula for calculating percentages:
Percentage = (Part / Whole) * 100
In our problem, the 'part' is 21, and the 'whole' is 84. Substituting these values into the formula, we get:
Percentage = (21 / 84) * 100
Percentage = 0.25 * 100
Percentage = 25
Again, this confirms that 21 is 25% of 84.
Method 3: Simplifying the Fraction
Before applying the percentage formula, we can simplify the fraction 21/84. Both the numerator and denominator are divisible by 21:
21/84 = (21 ÷ 21) / (84 ÷ 21) = 1/4
Now, converting the simplified fraction 1/4 to a percentage:
(1/4) * 100 = 25%
This method highlights the importance of simplifying fractions to make calculations easier and more efficient.
Practical Applications of Percentage Calculations
The ability to calculate percentages is crucial in various real-life situations:
1. Financial Calculations:
- Discounts: Calculating the price after a discount is applied. For example, a 20% discount on a $100 item means a saving of $20 (20% of $100).
- Interest Rates: Determining the interest earned on savings accounts or the interest paid on loans.
- Taxes: Calculating sales tax, income tax, or other taxes based on a percentage of the total amount.
- Profit Margins: Analyzing the profitability of a business by calculating the percentage of profit relative to revenue.
2. Data Analysis and Statistics:
- Representing Proportions: Showing the relative size of different groups within a dataset. For example, if a survey shows that 30% of respondents prefer a particular brand, this percentage provides a clear representation of that preference.
- Growth Rates: Calculating percentage increases or decreases in various quantities over time, such as population growth, economic growth, or stock prices.
3. Everyday Life:
- Tip Calculation: Calculating a tip in a restaurant based on a percentage of the bill amount.
- Grading System: Converting numerical scores to percentages in educational settings.
- Sales and Promotions: Understanding the actual savings offered during sales and promotional events.
Beyond the Basics: More Complex Percentage Problems
While the problem "What percent of 84 is 21?" represents a fundamental percentage calculation, understanding the underlying principles allows you to tackle more complex scenarios. Here are some examples:
- Finding the whole given the percentage and part: If 25% of a number is 21, what is the number? (Solution: 84)
- Finding the part given the percentage and whole: What is 15% of 60? (Solution: 9)
- Calculating percentage change: A product increased from $50 to $60. What is the percentage increase? (Solution: 20%)
- Compounding percentages: Calculating the final value after applying multiple percentage changes successively.
Mastering Percentage Calculations: Tips and Tricks
- Practice regularly: The best way to master percentage calculations is through consistent practice. Work through various problems to build confidence and improve your speed and accuracy.
- Use different methods: Experiment with different methods (proportions, formulas, simplifying fractions) to find the approach that best suits your understanding and the specific problem.
- Visual aids: Diagrams and charts can help visualize percentages and make them easier to understand, particularly in complex scenarios.
- Utilize online calculators: While it's important to understand the underlying principles, online calculators can be useful for checking your work or handling more complex problems. However, always strive for a thorough understanding of the process, not just the answer.
Conclusion: The Power of Percentages
The ability to calculate percentages is a valuable skill with wide-ranging applications. Understanding the principles outlined in this guide will enable you to confidently solve percentage problems, analyze data, and make informed decisions in various aspects of your life, both personal and professional. Remember that consistent practice is key to mastering this fundamental mathematical skill, and don't hesitate to explore different methods to find the one that best suits your learning style. From simple calculations like determining what percent of 84 is 21 to more complex financial or statistical analyses, understanding percentages provides a powerful tool for navigating the numerical world around us.
Latest Posts
Latest Posts
-
What Is The Percentage Of 0 25
Apr 03, 2025
-
How To Find The Slope Of Demand Curve
Apr 03, 2025
-
How Did He Know That The Nucleus Was Positively Charged
Apr 03, 2025
-
What Is 4 To The 5 Power
Apr 03, 2025
-
Integral 1 X 2 3 2
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 84 Is 21 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
