Integral 1 X 2 3 2
listenit
Apr 03, 2025 · 5 min read
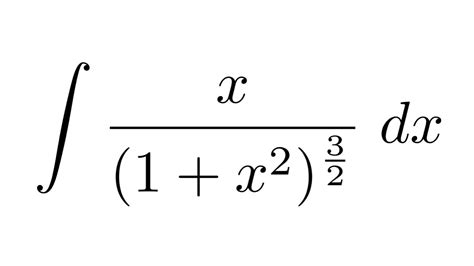
Table of Contents
Decoding the Mystery: A Deep Dive into the Integral of x^(2/3)
The seemingly simple integral ∫x^(2/3) dx might appear straightforward at first glance, but it unveils a fascinating journey into the world of calculus, revealing nuances in power rule application and offering valuable insights into integration techniques. This comprehensive guide will meticulously unravel the solution, exploring the underlying concepts, potential pitfalls, and practical applications. We'll also delve into related integrals and explore how this specific integral serves as a building block for more complex calculations.
Understanding the Power Rule of Integration
Before tackling the integral ∫x^(2/3) dx, let's revisit the fundamental power rule of integration. This rule states that the integral of xⁿ dx, where n is any real number except -1, is given by:
∫xⁿ dx = (xⁿ⁺¹)/(n+1) + C
where 'C' represents the constant of integration. This constant accounts for the fact that the derivative of a constant is zero, meaning multiple functions can have the same derivative.
Applying the Power Rule to ∫x^(2/3) dx
In our case, n = 2/3. Applying the power rule directly, we get:
∫x^(2/3) dx = (x^(2/3 + 1))/(2/3 + 1) + C
Simplifying the exponent and the denominator:
2/3 + 1 = 5/3
Therefore:
∫x^(2/3) dx = (x^(5/3))/(5/3) + C
Further simplification gives us the final result:
∫x^(2/3) dx = (3/5)x^(5/3) + C
Why the Constant of Integration (C) is Crucial
The constant of integration, 'C', is an essential part of the indefinite integral. It represents a family of functions, all of which have the same derivative. For example, if we differentiate (3/5)x^(5/3) + 2, (3/5)x^(5/3) + 10, or (3/5)x^(5/3) - π, we always get x^(2/3). The constant of integration acknowledges this ambiguity in the reverse process of differentiation.
Visualizing the Integral: The Area Under the Curve
The definite integral of a function represents the signed area between the function's curve and the x-axis over a specified interval. For ∫x^(2/3) dx, the function f(x) = x^(2/3) is a curve that starts at the origin (0,0) and increases monotonically for positive x values. The integral calculates the area under this curve.
Definite Integrals and Their Applications
Let's consider a definite integral, where we evaluate the area under the curve between specific limits:
∫[a, b] x^(2/3) dx = [(3/5)x^(5/3)] from a to b = (3/5)b^(5/3) - (3/5)a^(5/3)
This calculation has practical applications in various fields:
- Physics: Calculating work done by a variable force.
- Engineering: Determining the volume of irregular solids.
- Economics: Modeling cumulative production or consumption.
- Probability and Statistics: Finding expected values and probabilities related to certain distributions.
Exploring Related Integrals and Extensions
The integral of x^(2/3) serves as a foundational example. Let's explore related integrals and how our understanding can extend to more complex scenarios:
-
∫xⁿ dx for other fractional exponents: The power rule remains valid for any rational or even irrational exponent (except -1).
-
Integrals involving fractional exponents and other functions: Consider integrals like ∫x^(2/3) * e^x dx. These require more advanced integration techniques such as integration by parts or substitution.
-
Multiple integrals: The concept extends to multiple integrals, where we integrate over multiple variables. For instance, a double integral of x^(2/3)y^m over a specific region would involve integrating with respect to x and then y (or vice versa), using techniques of iterated integration.
Potential Pitfalls and Common Mistakes
While applying the power rule seems straightforward, several common mistakes can arise:
-
Incorrect exponent addition: Carefully adding 1 to the exponent (2/3 + 1 = 5/3) is critical. A small error here leads to an entirely wrong result.
-
Forgetting the constant of integration (C): This omission is a frequent error, particularly in indefinite integrals. Remember, the constant of integration is essential for representing the complete family of antiderivatives.
-
Improper handling of negative exponents: The power rule has a specific exception for n = -1, where the integral becomes ln|x| + C.
Numerical Methods for Approximating the Integral
When the antiderivative is difficult or impossible to find analytically, numerical methods offer a powerful alternative for approximating definite integrals. Methods like the trapezoidal rule, Simpson's rule, and Monte Carlo methods provide accurate estimates of the integral's value. These methods become crucial when dealing with complicated functions or when analytical solutions are unattainable.
Advanced Techniques and Further Exploration
For more intricate integrals involving x^(2/3), more sophisticated techniques may be necessary:
-
Integration by Parts: If the integrand is a product of functions, integration by parts is a valuable technique to simplify the integral.
-
Substitution: This method involves changing the variable of integration to simplify the expression.
Conclusion: Mastering the Fundamentals and Expanding Horizons
The seemingly simple integral ∫x^(2/3) dx offers a rich learning opportunity. Mastering the power rule, understanding the significance of the constant of integration, and appreciating the applications of definite integrals are crucial foundational concepts in calculus. This exploration not only provides a deep understanding of a basic integral but also lays the groundwork for tackling more complex integration problems, numerical approximations, and advanced calculus concepts. By carefully following the steps and understanding the underlying principles, you can confidently navigate the world of integration and apply it to a wide range of mathematical and real-world challenges. The journey of understanding this single integral is a testament to the beauty and power of calculus – a seemingly simple problem, upon closer examination, unlocks a wealth of mathematical concepts and applications.
Latest Posts
Latest Posts
-
What Is The Conjugate Base For H2s
Apr 08, 2025
-
5 Out Of 6 As A Percent
Apr 08, 2025
-
Does A Trapezoid Have 4 Right Angles
Apr 08, 2025
-
The Central Part Of An Atom Containing Protons And Neutrons
Apr 08, 2025
-
Position The Following Items In Order Of Decreasing Size
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about Integral 1 X 2 3 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.