How To Find The Slope Of Demand Curve
listenit
Apr 03, 2025 · 6 min read
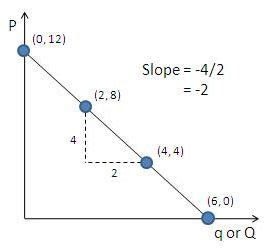
Table of Contents
How to Find the Slope of a Demand Curve: A Comprehensive Guide
The slope of the demand curve is a crucial concept in economics, representing the responsiveness of quantity demanded to changes in price. Understanding how to find it is vital for analyzing market dynamics, predicting consumer behavior, and making informed business decisions. This comprehensive guide will walk you through various methods, from simple calculations to advanced techniques handling real-world complexities.
Understanding the Demand Curve and its Slope
Before diving into calculations, let's solidify our understanding of the demand curve itself. The demand curve graphically depicts the relationship between the price of a good or service and the quantity demanded at each price point, ceteris paribus (all other factors being equal). It typically slopes downward, reflecting the law of demand: as price increases, quantity demanded decreases, and vice versa.
The slope of the demand curve quantifies this relationship, indicating the rate of change in quantity demanded for each unit change in price. A steeper slope suggests a less responsive demand (inelastic), while a flatter slope indicates a more responsive demand (elastic).
Method 1: Using Two Points on the Demand Curve
The most straightforward method for determining the slope involves selecting two points on the demand curve and applying the basic slope formula from algebra:
Slope = (Change in Quantity Demanded) / (Change in Price)
Or, more formally:
Slope = (Q₂ - Q₁) / (P₂ - P₁)
Where:
- Q₂ is the quantity demanded at the second point
- Q₁ is the quantity demanded at the first point
- P₂ is the price at the second point
- P₁ is the price at the first point
Example:
Let's say we have two points on a demand curve: (P₁, Q₁) = ($10, 100 units) and (P₂, Q₂) = ($8, 120 units).
Using the formula:
Slope = (120 - 100) / (8 - 10) = 20 / -2 = -10
The slope of the demand curve in this example is -10. The negative sign indicates the inverse relationship between price and quantity demanded – a characteristic feature of downward-sloping demand curves.
Method 2: Using the Demand Equation
Many times, the demand relationship is expressed as an equation. This provides a more precise and versatile way to calculate the slope. A typical linear demand equation takes the form:
Q = a - bP
Where:
- Q represents the quantity demanded
- P represents the price
- a represents the quantity demanded when the price is zero (vertical intercept)
- b represents the slope of the demand curve
In this equation, -b is the slope of the demand curve. The negative sign reflects the inverse relationship between price and quantity.
Example:
Consider the demand equation: Q = 200 - 20P
In this case, the slope (b) is -20. Therefore, the slope of the demand curve is -20. This means that for every one-unit increase in price, the quantity demanded decreases by 20 units.
Method 3: Analyzing a Demand Schedule (Table)
A demand schedule presents the relationship between price and quantity demanded in tabular format. While not directly providing a slope value, it allows you to calculate it using the two-point method.
Example:
| Price ($) | Quantity Demanded |
|---|---|
| 5 | 150 |
| 10 | 100 |
| 15 | 50 |
Select any two points from the schedule. For instance, let's use (10, 100) and (5, 150). Applying the formula:
Slope = (150 - 100) / (5 - 10) = 50 / -5 = -10
The slope is -10.
Handling Non-Linear Demand Curves
The methods described above primarily apply to linear demand curves. However, demand curves in the real world are often non-linear. For non-linear curves, the slope isn't constant. The slope at any specific point on a non-linear demand curve is determined using calculus, specifically the derivative.
The derivative of the demand function with respect to price gives the slope at a particular point.
Example:
Let's assume a non-linear demand function: Q = 100 - 5P + P²
To find the slope at a specific point, say P = 5, we first find the derivative:
dQ/dP = -5 + 2P
Now, substitute P = 5 into the derivative:
dQ/dP = -5 + 2(5) = 5
The slope at P = 5 is 5. Note that unlike linear functions, the slope here is positive, implying an unusual upward-sloping section of the demand curve which is rarely found in typical market scenarios for most goods and services but possible for Giffen goods or Veblen goods.
Interpreting the Slope's Magnitude and Sign
The magnitude and sign of the slope carry important implications:
-
Magnitude: A larger absolute value of the slope (e.g., -20) indicates a steeper curve and less elastic demand. A smaller absolute value (e.g., -2) indicates a flatter curve and more elastic demand.
-
Sign: The negative sign is typical for normal demand curves, reflecting the inverse relationship between price and quantity demanded. A positive slope (though uncommon for most goods) would suggest a Giffen good, where increased price leads to increased quantity demanded (due to income effects overwhelming substitution effects).
Factors Affecting the Slope of the Demand Curve
Several factors influence the slope, making it a dynamic measure:
-
Availability of substitutes: Goods with many close substitutes tend to have more elastic demand (flatter slope), as consumers readily switch to alternatives if the price rises.
-
Necessity vs. luxury: Necessities typically have less elastic demand (steeper slope) than luxury goods. People are less likely to reduce consumption of necessities even if prices increase.
-
Time horizon: Demand tends to be more elastic in the long run than in the short run. Consumers have more time to adjust their consumption patterns and find alternatives.
-
Proportion of income: Goods representing a larger proportion of a consumer's income tend to have more elastic demand. A price increase for a significant portion of a budget will have a more noticeable impact on consumption choices.
-
Consumer preferences and tastes: Changing tastes and preferences can shift the demand curve and alter its slope.
Advanced Techniques and Considerations
For more complex scenarios involving multiple goods or factors, advanced econometric techniques such as regression analysis are often employed to estimate the demand curve and its slope. These methods use statistical tools to analyze data and determine the relationship between price and quantity demanded, controlling for other influencing variables.
Conclusion: Mastering Demand Curve Slope Analysis
Understanding how to find the slope of the demand curve is fundamental to economic analysis. Whether employing basic algebraic methods or more advanced calculus and econometric techniques, the process provides valuable insights into market behavior and informs strategic decision-making in various contexts, from pricing strategies to public policy interventions. Remember that the slope is not a static measure; it reflects a dynamic relationship influenced by several factors, making continuous monitoring and analysis crucial. By mastering these techniques, you will be well-equipped to interpret market dynamics and leverage this knowledge for informed action.
Latest Posts
Latest Posts
-
Boron Is Solid Liquid Or Gas
Apr 04, 2025
-
What Is The Greatest Common Factor Of 36 And 60
Apr 04, 2025
-
How Do You Graph Y 3x 4
Apr 04, 2025
-
Is Ch3oh An Acid Or Base
Apr 04, 2025
-
How Many Isotopes Does Argon Have
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about How To Find The Slope Of Demand Curve . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
