What Is Square Root Of 40
listenit
Mar 29, 2025 · 5 min read
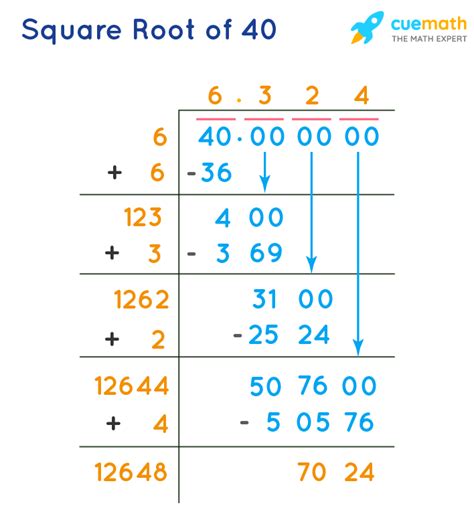
Table of Contents
What is the Square Root of 40? A Deep Dive into Square Roots and Their Applications
The seemingly simple question, "What is the square root of 40?", opens a door to a fascinating world of mathematics, encompassing concepts far beyond a simple numerical answer. While a calculator readily provides an approximate decimal value, understanding the underlying principles, methods of calculation, and the broader applications of square roots offers a richer and more insightful understanding. This article will delve into these aspects, exploring the square root of 40 in detail and uncovering its relevance in various fields.
Understanding Square Roots
Before we tackle the square root of 40 specifically, let's establish a firm grasp of the fundamental concept of square roots. The square root of a number is a value that, when multiplied by itself (squared), gives the original number. In mathematical notation, the square root of a number 'x' is denoted as √x.
For example:
- √9 = 3 because 3 * 3 = 9
- √16 = 4 because 4 * 4 = 16
- √25 = 5 because 5 * 5 = 25
Calculating the Square Root of 40: Methods and Approximations
Unlike perfect squares (numbers with integer square roots, like 9, 16, 25), 40 does not have a whole number square root. This means its square root is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation continues infinitely without repeating.
Several methods can be used to approximate the square root of 40:
1. Using a Calculator
The simplest and most direct method is using a calculator. Most calculators have a dedicated square root function (√). Entering √40 will yield an approximate value of 6.32455532. This is a convenient approach for quick calculations, but it doesn't provide insight into the mathematical process.
2. The Babylonian Method (or Heron's Method)
This iterative method provides a progressively more accurate approximation of the square root. It involves the following steps:
-
Start with an initial guess: Let's guess 6, as 6² = 36, which is close to 40.
-
Improve the guess: Divide the number (40) by the initial guess (6): 40/6 ≈ 6.6667
-
Average the guess and the result: Average the initial guess (6) and the result (6.6667): (6 + 6.6667)/2 ≈ 6.3333
-
Repeat steps 2 and 3: Use the new guess (6.3333) and repeat the process. With each iteration, the approximation improves.
Continuing this process several times will yield a highly accurate approximation of the square root of 40.
3. Estimation through Perfect Squares
We can estimate the square root of 40 by considering the nearest perfect squares:
- 6² = 36
- 7² = 49
Since 40 lies between 36 and 49, its square root must be between 6 and 7. This provides a rough estimation, useful for quick mental calculations.
The Square Root of 40 in Different Contexts
The square root of 40, while seemingly a simple mathematical concept, finds applications across numerous fields:
1. Geometry and Trigonometry
Square roots frequently appear in geometrical calculations, particularly when dealing with distances, areas, and volumes. For example, if the area of a square is 40 square units, the length of its side is √40 units. Similarly, trigonometric functions often involve square roots in their calculations.
2. Physics and Engineering
Numerous physics and engineering formulas incorporate square roots. For instance, calculating the velocity of an object, the period of a pendulum, or the impedance in an electrical circuit often necessitates the use of square roots.
3. Statistics and Data Analysis
Standard deviation, a crucial measure of data dispersion in statistics, involves the square root of the variance. This helps quantify the spread of data points around the mean.
4. Computer Graphics and Game Development
In computer graphics, square roots are frequently used in distance calculations, transformations, and simulations. For example, determining the distance between two points on a screen often involves the Pythagorean theorem, which incorporates square roots.
5. Financial Modeling
Financial models frequently utilize square roots in calculating risk measures such as standard deviation and variance, which are critical in assessing investment portfolio performance and risk management.
Beyond the Decimal Approximation: Exploring the Irrational Nature of √40
Understanding that the square root of 40 is irrational adds another layer of depth to its nature. Irrational numbers are numbers that cannot be expressed as a ratio of two integers. Their decimal representations are non-terminating and non-repeating. This seemingly abstract concept has profound implications:
-
Infinite Decimal Expansion: The decimal representation of √40 goes on forever without ever settling into a repeating pattern. This highlights the inherent complexity of irrational numbers.
-
Geometric Representation: The irrationality of √40 can be visualized geometrically. Imagine trying to construct a square with an area of exactly 40 square units. You cannot do so using only a ruler and compass, as the side length would be √40 units – an irrational number.
-
Approximation and Error: Since we can only approximate √40, there is always an inherent error in our calculations. The precision of the approximation depends on the method used and the number of iterations (in methods like the Babylonian method). This concept is crucial in many applications where the level of accuracy must be carefully considered.
Simplifying Square Roots: Prime Factorization and Radicals
Although √40 doesn't simplify to a whole number, we can simplify it algebraically using prime factorization. The prime factorization of 40 is 2³ * 5. Therefore:
√40 = √(2³ * 5) = √(2² * 2 * 5) = 2√(2 * 5) = 2√10
This simplified form, 2√10, is often more useful in algebraic manipulations and problem-solving than the decimal approximation. This highlights the importance of understanding both numerical and algebraic representations of square roots.
Conclusion: The Square Root of 40 – More Than Just a Number
The seemingly simple question, "What is the square root of 40?", leads us on a journey through fundamental mathematical concepts, calculation techniques, and various real-world applications. From understanding the properties of irrational numbers to applying square roots in diverse fields, this exploration underscores the significance of this seemingly simple mathematical function. Whether utilizing a calculator for quick approximations or employing more sophisticated methods like the Babylonian method, a deep understanding of square roots enhances our problem-solving capabilities and broadens our appreciation of mathematics' pervasive influence on our world. This detailed exploration moves beyond a simple numerical answer, revealing the rich tapestry woven by this fundamental mathematical concept.
Latest Posts
Latest Posts
-
Does A Gas Have A Definite Shape And Volume
Mar 31, 2025
-
Factor X 3 X 2 2
Mar 31, 2025
-
How Many Neutrons Does Uranium 238 Have
Mar 31, 2025
-
Does Ccl4 Have Dipole Dipole Forces
Mar 31, 2025
-
Is Wood Rotting A Physical Or Chemical Change
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is Square Root Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
