Factor X 3 X 2 2
listenit
Mar 31, 2025 · 5 min read
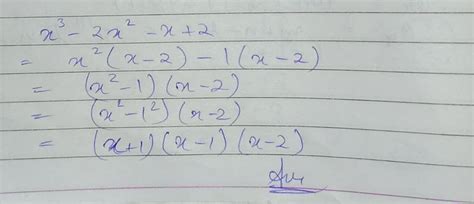
Table of Contents
Decoding Factor X: A Deep Dive into 3x² + 2x + 2
The expression "3x² + 2x + 2" might seem like a simple algebraic equation, but it represents a gateway to a vast world of mathematical concepts. This seemingly straightforward quadratic expression opens doors to discussions of factoring, solving quadratic equations, graphing parabolas, and even delving into more advanced topics like complex numbers. This article will explore this expression in detail, covering various aspects and providing a comprehensive understanding of its significance in algebra and beyond.
Understanding Quadratic Expressions: A Foundation
Before diving into the specifics of 3x² + 2x + 2, let's establish a firm foundation by understanding the basics of quadratic expressions. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (in this case, x) is 2. The general form of a quadratic expression is ax² + bx + c, where 'a', 'b', and 'c' are constants (numbers). In our specific expression, 3x² + 2x + 2, we have a = 3, b = 2, and c = 2.
The Significance of the Coefficients
The coefficients (a, b, and c) play a crucial role in determining the properties of the quadratic expression. They influence the shape of the parabola when graphed, the location of its vertex, and the roots (or solutions) of the corresponding quadratic equation. In our case, the positive value of 'a' (a = 3) indicates that the parabola opens upwards, meaning it has a minimum value.
Factoring the Quadratic Expression
One of the key operations in algebra is factoring, which involves expressing an algebraic expression as a product of simpler expressions. Factoring simplifies expressions, allowing for easier manipulation and problem-solving. However, not all quadratic expressions can be easily factored using integers. Let's explore the possibilities for factoring 3x² + 2x + 2.
Attempting Integer Factoring
We can attempt to factor 3x² + 2x + 2 by looking for two binomials that, when multiplied, result in the original expression. We seek numbers that multiply to 3 (the coefficient of x²) and add up to 2 (the coefficient of x). Unfortunately, there are no two integers that satisfy this condition. This indicates that the expression 3x² + 2x + 2 is not factorable using integers.
Exploring Other Factoring Methods
Since integer factoring isn't feasible, we can explore other methods. We could use the quadratic formula, which provides a general solution for solving quadratic equations. This method will be discussed later in the article.
Solving the Quadratic Equation: Finding the Roots
The expression 3x² + 2x + 2 becomes a quadratic equation when set equal to zero: 3x² + 2x + 2 = 0. Solving this equation means finding the values of 'x' that satisfy the equation – these values are called the roots or solutions of the equation.
The Quadratic Formula: A Powerful Tool
The quadratic formula is a universal method for solving quadratic equations of the form ax² + bx + c = 0. The formula is given by:
x = [-b ± √(b² - 4ac)] / 2a
Substituting the values from our equation (a = 3, b = 2, c = 2), we get:
x = [-2 ± √(2² - 4 * 3 * 2)] / (2 * 3) x = [-2 ± √(4 - 24)] / 6 x = [-2 ± √(-20)] / 6
Notice that we have a negative number under the square root. This indicates that the roots of this quadratic equation are complex numbers, involving the imaginary unit 'i', where i² = -1.
Understanding Complex Numbers
Complex numbers are numbers of the form a + bi, where 'a' and 'b' are real numbers, and 'i' is the imaginary unit. The presence of complex roots signifies that the parabola represented by the equation 3x² + 2x + 2 does not intersect the x-axis.
Calculating the Complex Roots
Simplifying the expression for 'x', we obtain the complex roots:
x = [-2 ± √(20)i] / 6 x = [-2 ± 2√(5)i] / 6 x = [-1 ± √(5)i] / 3
Therefore, the roots of the quadratic equation 3x² + 2x + 2 = 0 are x = (-1 + √5i)/3 and x = (-1 - √5i)/3.
Graphing the Parabola
The quadratic expression 3x² + 2x + 2 can be represented graphically as a parabola. The parabola's shape, vertex, and axis of symmetry are determined by the coefficients of the expression.
Key Features of the Parabola
- Vertex: The vertex represents the minimum point of the parabola since 'a' is positive. The x-coordinate of the vertex can be found using the formula -b/2a, which gives -2/(2*3) = -1/3. The y-coordinate can be found by substituting this x-value back into the original expression.
- Axis of Symmetry: The axis of symmetry is a vertical line passing through the vertex. Its equation is x = -1/3.
- Concavity: Since a = 3 (positive), the parabola opens upwards.
- x-intercepts: As we found earlier, the parabola does not intersect the x-axis because the roots are complex numbers.
- y-intercept: The y-intercept is the point where the parabola crosses the y-axis. This occurs when x = 0. Substituting x = 0 into the expression, we get y = 2. Therefore, the y-intercept is (0, 2).
Applications and Extensions
The expression 3x² + 2x + 2, although seemingly simple, has applications in various areas, including:
Physics and Engineering
Quadratic equations are frequently used to model projectile motion, where the height of an object over time follows a parabolic path. Similar applications exist in engineering for analyzing the strength of structures and designing optimal shapes.
Economics and Finance
Quadratic functions can represent cost, revenue, or profit models, allowing economists and financial analysts to determine optimal production levels or investment strategies.
Computer Science and Algorithms
Quadratic equations and related algorithms are used in computer graphics, optimization problems, and search algorithms.
Further Exploration: Completing the Square and Other Methods
While we've primarily focused on the quadratic formula, other methods exist for solving quadratic equations, such as completing the square and using graphical methods. Completing the square involves manipulating the expression to create a perfect square trinomial, allowing for easier factorization and solution.
Conclusion: A Multifaceted Expression
The seemingly simple expression 3x² + 2x + 2 reveals a rich tapestry of mathematical concepts, encompassing factoring, solving quadratic equations, understanding complex numbers, and graphing parabolas. Its applications extend far beyond the realm of pure mathematics, making it a fundamental building block in various fields of science, engineering, and economics. Understanding this expression and the associated techniques provides a strong foundation for tackling more complex mathematical problems and fosters a deeper appreciation for the elegance and power of algebra. This comprehensive exploration underscores the importance of delving deeper into seemingly simple mathematical expressions to uncover their hidden depths and wider significance.
Latest Posts
Latest Posts
-
What Is The Square Root Of 122
Apr 02, 2025
-
The Unit Of Energy In Si Units Is
Apr 02, 2025
-
How To Find The Mean Of A Probability Distribution
Apr 02, 2025
-
How Do Producers Get Their Energy
Apr 02, 2025
-
The Number Of Protons In An Atom Is That Elements
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Factor X 3 X 2 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
