If Pressure Increases What Happens To Volume
listenit
Apr 02, 2025 · 5 min read
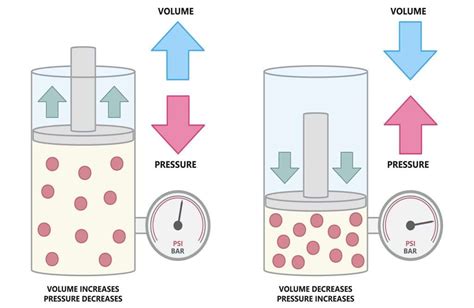
Table of Contents
If Pressure Increases, What Happens to Volume? Understanding the Inverse Relationship
The relationship between pressure and volume is a fundamental concept in physics, particularly within the realm of thermodynamics and fluid mechanics. Understanding how changes in pressure affect volume is crucial in various applications, from designing engines and hydraulic systems to predicting weather patterns and comprehending biological processes. This comprehensive guide delves deep into the relationship between pressure and volume, exploring the underlying principles, relevant laws, and real-world examples.
Boyle's Law: The Foundation of Pressure-Volume Relationship
The cornerstone of understanding how pressure and volume interact is Boyle's Law. This law, formulated by Robert Boyle in the 17th century, states that for a fixed amount of gas at a constant temperature, the pressure (P) and volume (V) are inversely proportional. Mathematically, this is represented as:
P₁V₁ = P₂V₂
where:
- P₁ and V₁ represent the initial pressure and volume
- P₂ and V₂ represent the final pressure and volume
This equation means that if you increase the pressure on a gas, its volume will decrease proportionally, and vice versa. This inverse relationship holds true under ideal conditions, meaning the gas behaves ideally and doesn't experience intermolecular forces or significant deviations from ideal gas behavior.
Understanding the Inverse Proportionality
The inverse proportionality means that the product of pressure and volume remains constant. If you double the pressure, the volume will be halved. If you triple the pressure, the volume will be reduced to one-third. This relationship is beautifully illustrated by imagining a gas trapped in a cylinder with a movable piston. Pushing down on the piston (increasing pressure) will compress the gas, reducing its volume. Conversely, pulling the piston upwards (decreasing pressure) will allow the gas to expand, increasing its volume.
Ideal Gas Law: A More Comprehensive Perspective
While Boyle's Law provides a good foundation, it's a simplification. The Ideal Gas Law provides a more comprehensive description of the relationship between pressure, volume, temperature, and the amount of gas present. The Ideal Gas Law is expressed as:
PV = nRT
where:
- P = Pressure
- V = Volume
- n = Number of moles of gas
- R = Ideal gas constant
- T = Temperature (in Kelvin)
This equation shows that pressure and volume are still inversely related, but the relationship is now influenced by the number of gas molecules (n) and the temperature (T). Keeping 'n' and 'T' constant, the equation reduces to Boyle's Law.
Implications of the Ideal Gas Law
The Ideal Gas Law highlights that changes in pressure will affect volume differently depending on the temperature and the amount of gas. For instance, if you increase the pressure on a gas while keeping the temperature constant, the volume will decrease. However, if you increase the temperature while maintaining constant pressure, the volume will increase. The Ideal Gas Law elegantly combines Boyle's Law with Charles's Law (relating volume and temperature) and Avogadro's Law (relating volume and the number of moles).
Real Gases: Departures from Ideality
It's important to note that the Ideal Gas Law is an approximation. Real gases, particularly at high pressures and low temperatures, deviate from ideal behavior. Intermolecular forces (attractive and repulsive forces between gas molecules) become significant at higher pressures and lower temperatures, influencing the gas's volume and pressure more than predicted by the ideal gas law.
Compressibility Factor
The compressibility factor (Z) is a dimensionless quantity used to quantify the deviation of a real gas from ideal gas behavior. Z is defined as:
Z = PV/nRT
For an ideal gas, Z = 1. For real gases, Z can be greater than or less than 1, depending on the pressure, temperature, and the type of gas. A Z value greater than 1 indicates that the gas is more compressible than an ideal gas, while a Z value less than 1 indicates that the gas is less compressible than an ideal gas.
Real-World Applications: Seeing the Pressure-Volume Relationship in Action
The pressure-volume relationship has wide-ranging practical applications across numerous fields:
1. Automotive Engines:
Internal combustion engines rely heavily on the pressure-volume relationship. The compression stroke increases the pressure of the air-fuel mixture, significantly decreasing its volume. This compressed mixture then ignites, causing a rapid expansion (increase in volume) that drives the piston.
2. Hydraulic Systems:
Hydraulic systems, such as those used in construction equipment and braking systems, utilize the principle of Pascal's Law, which states that a change in pressure applied to an enclosed incompressible fluid is transmitted undiminished to all portions of the fluid and to the walls of the containing vessel. By applying pressure to a small area, a larger force can be exerted on a larger area, allowing for mechanical advantage.
3. Weather Forecasting:
Atmospheric pressure and volume changes play a critical role in weather patterns. High-pressure systems are associated with sinking air and generally clear skies, while low-pressure systems are characterized by rising air and often stormy weather.
4. Deep-Sea Diving:
Divers experience increased pressure with depth due to the weight of the water above them. This increased pressure causes a decrease in the volume of air in their lungs and other air spaces in the body. Understanding this relationship is critical for diver safety.
5. Medical Applications:
In medicine, understanding pressure-volume relationships is crucial in various contexts, including ventilation in respiratory therapy, the functioning of the cardiovascular system (blood pressure and blood flow), and the behavior of gases within the body.
Conclusion: A Dynamic Relationship with Real-World Implications
The relationship between pressure and volume, as elegantly described by Boyle's Law and more comprehensively by the Ideal Gas Law, is a cornerstone of physics and has profound implications in numerous fields. While the inverse relationship simplifies much, the influence of temperature and intermolecular forces in real gases necessitates a more nuanced understanding provided by the Ideal Gas Law and the concept of the compressibility factor. Recognizing how pressure affects volume is key to comprehending and manipulating systems from tiny biological mechanisms to massive engineering projects. The inverse pressure-volume relationship isn't just a theoretical concept; it's a fundamental force shaping the world around us.
Latest Posts
Latest Posts
-
Whats The Square Root Of 56
Apr 03, 2025
-
What Are The Common Factors Of 6 And 15
Apr 03, 2025
-
What Is The Sqaure Root Of 196
Apr 03, 2025
-
How Many Electrons Can Fit In The First Energy Level
Apr 03, 2025
-
The Basic Unit Of A Chemical Element
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about If Pressure Increases What Happens To Volume . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
