What Are The Common Factors Of 6 And 15
listenit
Apr 03, 2025 · 5 min read
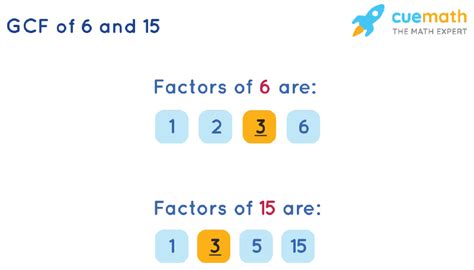
Table of Contents
What are the Common Factors of 6 and 15? A Deep Dive into Number Theory
Finding the common factors of two numbers might seem like a simple task, especially for smaller numbers like 6 and 15. However, understanding this concept lays the foundation for more complex number theory concepts, such as the greatest common divisor (GCD) and least common multiple (LCM). This article will not only answer the question of what the common factors of 6 and 15 are but will also delve into the underlying mathematical principles, exploring various methods to find these factors and demonstrating their practical applications.
Understanding Factors and Common Factors
Before we dive into the specifics of 6 and 15, let's define some key terms. A factor (or divisor) of a number is a whole number that divides evenly into that number without leaving a remainder. For example, the factors of 6 are 1, 2, 3, and 6, because each of these numbers divides 6 without leaving a remainder. Similarly, the factors of 15 are 1, 3, 5, and 15.
Common factors, as the name suggests, are the factors that two or more numbers share. They are the numbers that divide evenly into both numbers. Identifying these common factors is crucial in various mathematical operations and real-world applications.
Finding the Common Factors of 6 and 15
There are several ways to determine the common factors of 6 and 15:
1. Listing the Factors: A Simple Approach
The most straightforward method is to list all the factors of each number and then identify the ones they have in common.
- Factors of 6: 1, 2, 3, 6
- Factors of 15: 1, 3, 5, 15
By comparing these lists, we can see that the common factors of 6 and 15 are 1 and 3.
2. Prime Factorization: A More Systematic Approach
Prime factorization involves expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves). This method is particularly useful for larger numbers.
- Prime factorization of 6: 2 x 3
- Prime factorization of 15: 3 x 5
The common prime factor in both factorizations is 3. Since 1 is a factor of every number, 1 and 3 are the common factors.
3. Venn Diagrams: A Visual Representation
Venn diagrams offer a visual way to compare the factors of two or more numbers. We can represent the factors of each number in separate circles, with the overlapping area showing the common factors.
[Imagine a Venn diagram here with one circle labeled "Factors of 6" containing 1, 2, 3, 6 and another circle labeled "Factors of 15" containing 1, 3, 5, 15. The overlapping area contains 1 and 3.]
This visual representation clearly shows that the common factors of 6 and 15 are 1 and 3.
Greatest Common Divisor (GCD)
The greatest common divisor (GCD), also known as the highest common factor (HCF), is the largest number that divides both numbers without leaving a remainder. In the case of 6 and 15, the GCD is 3. Understanding the GCD is essential in simplifying fractions and solving various mathematical problems.
Applications of Common Factors and GCD
The concept of common factors and the GCD has numerous applications across various fields:
1. Simplifying Fractions
When simplifying fractions, we divide both the numerator and the denominator by their GCD. For example, the fraction 6/15 can be simplified to 2/5 by dividing both the numerator (6) and the denominator (15) by their GCD, which is 3.
2. Solving Word Problems
Many word problems involving ratios, proportions, and distribution require finding common factors or the GCD. For example, consider a problem where you need to divide 6 apples and 15 oranges equally among several people. The GCD (3) determines the maximum number of people you can divide the fruit amongst evenly.
3. Geometry and Measurement
Common factors are crucial in geometry when dealing with problems involving area, perimeter, and scaling. For example, if you have a rectangle with sides of 6 units and 15 units, the GCD helps determine the size of the largest square that can tile the rectangle without any gaps or overlaps.
4. Modular Arithmetic and Cryptography
In modular arithmetic, which forms the basis of many modern cryptographic systems, finding the GCD plays a significant role in determining the invertibility of elements and solving congruences.
Beyond 6 and 15: Extending the Concepts
The principles discussed above apply to any pair of numbers. Let's consider a more complex example: finding the common factors of 24 and 36.
- Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
- Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
The common factors are 1, 2, 3, 4, 6, and 12. The GCD is 12.
Using prime factorization:
- Prime factorization of 24: 2³ x 3
- Prime factorization of 36: 2² x 3²
The common prime factors are 2² and 3, resulting in a GCD of 2² x 3 = 12.
Conclusion: The Importance of Understanding Common Factors
Understanding common factors and the greatest common divisor is fundamental to various areas of mathematics and its applications. While the concept might seem elementary at first, its implications extend far beyond simply finding factors of small numbers. Mastering this concept provides a solid base for tackling more complex mathematical problems and real-world scenarios involving ratios, proportions, geometry, and even cryptography. The methods outlined in this article—listing factors, prime factorization, and Venn diagrams—offer versatile tools to determine common factors, regardless of the size of the numbers involved. By utilizing these techniques and understanding the underlying principles, you can confidently navigate numerical challenges and appreciate the power of seemingly simple mathematical concepts.
Latest Posts
Latest Posts
-
Mars Distance From Earth In Light Years
Apr 04, 2025
-
What Energy Transformation Takes Place During Photosynthesis
Apr 04, 2025
-
What Does A Higher Specific Heat Mean
Apr 04, 2025
-
Question Plane Draw The Skeletal Structures
Apr 04, 2025
-
100 Yards On A Football Field
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Are The Common Factors Of 6 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
