What's The Square Root Of 56
listenit
Apr 03, 2025 · 5 min read
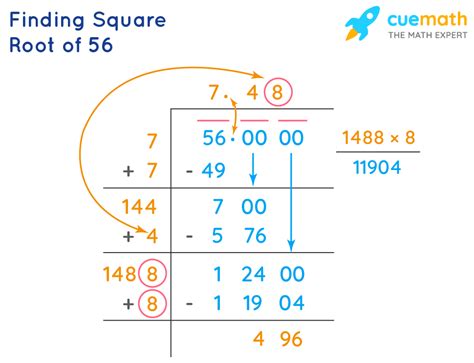
Table of Contents
What's the Square Root of 56? Unpacking the Calculation and its Applications
The seemingly simple question, "What's the square root of 56?", opens a door to a fascinating exploration of mathematics, encompassing various calculation methods, practical applications, and the broader context of square roots within the realm of numbers. While a calculator readily provides an approximate decimal value, understanding the underlying concepts enhances mathematical comprehension and problem-solving skills.
Understanding Square Roots
Before diving into the specifics of the square root of 56, let's solidify our understanding of what a square root actually represents. The square root of a number (x) is a value that, when multiplied by itself, equals x. In simpler terms, it's the inverse operation of squaring a number. For example, the square root of 9 (√9) is 3, because 3 * 3 = 9.
This seemingly straightforward concept extends to numbers beyond perfect squares—numbers that have whole number square roots. Numbers like 56 don't have neat, whole-number square roots. This leads us to different methods for calculating and approximating the square root of 56.
Methods for Calculating √56
Several approaches exist for finding the square root of 56, each with its own advantages and disadvantages:
1. Using a Calculator: The simplest and most efficient method is using a calculator. Most scientific calculators have a dedicated square root function (√). Inputting 56 and pressing the square root button yields an approximate value of 7.4833147735. This is the most practical approach for most everyday applications.
2. Estimation and Approximation: For situations where a calculator isn't available, estimation offers a valuable skill. We know that 7² = 49 and 8² = 64. Since 56 falls between 49 and 64, the square root of 56 must be between 7 and 8. A reasonable initial estimate would be around 7.5. Refining this estimate requires iterative methods.
3. Babylonian Method (or Heron's Method): This iterative method refines an initial guess to converge on a more accurate approximation. The formula is:
xₙ₊₁ = ½(xₙ + S/xₙ)
where:
- xₙ is the current approximation
- xₙ₊₁ is the next, improved approximation
- S is the number whose square root is being calculated (in this case, 56)
Let's illustrate with an initial guess of 7.5:
- Iteration 1: x₁ = ½(7.5 + 56/7.5) ≈ 7.4833
- Iteration 2: x₂ = ½(7.4833 + 56/7.4833) ≈ 7.48331477
As you can see, the method rapidly converges on a highly accurate result. Each iteration provides a progressively closer approximation.
4. Long Division Method: A more complex method, suitable for demonstrating a deeper understanding of square root calculations, is the long division method. This is a manual process that involves breaking down the number into groups of digits and systematically finding the digits of the square root. While less efficient than the Babylonian method or calculator, understanding this method provides valuable insight into the mechanics of square root calculations. Detailed explanation of the long division method for calculating square roots is best presented in a separate, more comprehensive article.
The Irrational Nature of √56
It's crucial to understand that the square root of 56 is an irrational number. This means it cannot be expressed as a simple fraction (a ratio of two integers) and its decimal representation goes on forever without repeating. The decimal approximation we obtain (7.4833147735...) is only an approximation; the true value has infinitely many non-repeating digits.
Applications of Square Roots
Square roots find numerous applications across various fields:
1. Geometry: Calculating distances, areas, and volumes frequently involve square roots. The Pythagorean theorem (a² + b² = c²), used to find the length of the hypotenuse in a right-angled triangle, necessitates calculating square roots. Determining the diagonal of a square or rectangle also requires square root calculations.
2. Physics: Square roots appear in numerous physics formulas. For instance, calculating the speed of an object, the period of a pendulum, or the magnitude of a vector often involves square roots. The equations governing wave motion and the energy of a particle also rely on them.
3. Statistics: Standard deviation, a key measure of data dispersion, involves calculating the square root of the variance. Understanding variability and data distributions in statistics requires using square roots extensively.
4. Finance: Calculating compound interest, determining the present value of future payments, and understanding portfolio risk often rely on square root calculations. Many financial models and formulas use square roots for accurate estimations.
5. Computer Graphics and Game Development: Square roots are fundamental for various operations in computer graphics and game development. Calculations involving distances between points, vector normalization, and collision detection all depend heavily on square root computations.
6. Engineering: Numerous engineering calculations across various disciplines – civil, mechanical, electrical – incorporate square roots. Structural analysis, circuit design, and signal processing often necessitate the use of square roots.
Beyond √56: Expanding Mathematical Understanding
Understanding the square root of 56 isn't just about finding a numerical answer. It's about grasping the fundamental concept of square roots, exploring different calculation methods, appreciating the irrationality of numbers, and recognizing the widespread application of square roots in diverse fields. This seemingly simple mathematical operation underpins a vast range of practical applications, highlighting the interconnectedness of mathematical concepts and their relevance to the real world. The journey from a simple question to a comprehensive understanding of square roots exemplifies the beauty and power of mathematical exploration. Further exploration into related concepts like cube roots, higher-order roots, and complex numbers would further enhance one's mathematical foundation. The pursuit of mathematical knowledge is a continuous journey of discovery, and the square root of 56 serves as a small but significant step along that path.
Latest Posts
Latest Posts
-
What Does A Higher Specific Heat Mean
Apr 04, 2025
-
Question Plane Draw The Skeletal Structures
Apr 04, 2025
-
100 Yards On A Football Field
Apr 04, 2025
-
A Consumer That Eats Only Plants
Apr 04, 2025
-
The Amount Of Energy Required To Raise The Temperature
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What's The Square Root Of 56 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
