How To Find Perimeter With Area Given
listenit
Apr 01, 2025 · 6 min read
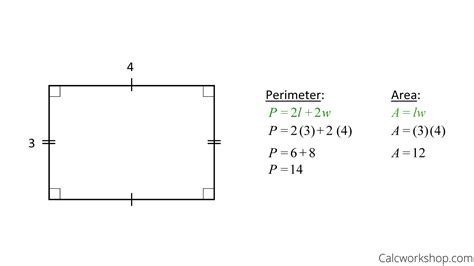
Table of Contents
How to Find Perimeter with Area Given: A Comprehensive Guide
Determining the perimeter of a shape when only the area is known presents a unique challenge in geometry. Unlike direct calculations where dimensions are provided, this inverse problem requires a deeper understanding of the relationships between area and perimeter for different shapes. This comprehensive guide will delve into various methods and scenarios, equipping you with the skills to tackle this intriguing mathematical puzzle. We will cover common geometric shapes and explore the limitations of this problem.
Understanding the Relationship Between Area and Perimeter
The fundamental concept to grasp is that area and perimeter are distinct yet interconnected properties of a geometric shape. Area measures the two-dimensional space enclosed within the shape's boundaries, while perimeter measures the total length of its boundary. Crucially, knowing the area alone is insufficient to determine the perimeter uniquely. This is because many shapes can share the same area but have different perimeters.
Let's illustrate this with a simple example: Consider two rectangles. One has dimensions 2 units by 4 units, and the other has dimensions 1 unit by 8 units. Both rectangles have an area of 8 square units. However, their perimeters differ: the first has a perimeter of 12 units (2(2+4)), while the second has a perimeter of 18 units (2(1+8)).
This highlights the critical point: additional information or constraints are necessary to solve for the perimeter when only the area is provided. This additional information might include:
- The shape of the figure: Knowing the shape (e.g., square, rectangle, circle, triangle) significantly constrains the possibilities.
- Specific ratios of sides: Information about the relationship between sides (e.g., a rectangle with sides in a 2:1 ratio).
- Other dimensions: Knowing even one side length helps immensely.
- Constraints on the shape: For instance, a rectangle with a maximum perimeter.
Solving for Perimeter with Area: Case Studies by Shape
Let's explore how to find the perimeter for several common geometric shapes when given their area.
1. Square
A square is the simplest case. Let 's' be the side length of the square. The area (A) and perimeter (P) are related as follows:
- Area (A) = s²
- Perimeter (P) = 4s
If the area is known, we can find 's' by taking the square root of the area: s = √A. Substituting this into the perimeter formula gives:
P = 4√A
Example: If a square has an area of 25 square units, its side length is √25 = 5 units, and its perimeter is 4 * 5 = 20 units.
2. Rectangle
Rectangles present a more complex scenario because they have two distinct side lengths. Let 'l' and 'w' represent the length and width, respectively.
- Area (A) = l * w
- Perimeter (P) = 2(l + w)
With only the area known, we have one equation with two unknowns. We need additional information. Suppose we know the ratio of length to width (e.g., l = 2w). Then:
A = 2w * w = 2w² w = √(A/2) l = 2√(A/2) = √(2A) P = 2(√(A/2) + √(2A))
Example: A rectangle has an area of 18 square units, and its length is twice its width. Then w = √(18/2) = 3 units, l = 6 units, and P = 2(3 + 6) = 18 units. Without the ratio information, an infinite number of rectangles could have an area of 18 square units.
3. Circle
For a circle, the area and perimeter (circumference) are related to the radius (r):
- Area (A) = πr²
- Circumference (C) = 2πr
From the area, we can find the radius: r = √(A/π). Substituting this into the circumference formula gives:
C = 2π√(A/π) = 2√(πA)
Example: A circle with an area of 25π square units has a radius of √(25π/π) = 5 units and a circumference of 2π(5) = 10π units.
4. Triangle
Finding the perimeter of a triangle given only its area is significantly more challenging. The area of a triangle is given by:
- Area (A) = (1/2)bh (where b is the base and h is the height)
Even with Heron's formula, which relates the area to the side lengths (a, b, c) through the semi-perimeter (s = (a+b+c)/2):
- A = √(s(s-a)(s-b)(s-c))
we still have a complex equation with three unknowns. We would need additional information about the sides or angles of the triangle to solve for its perimeter.
5. Other Shapes
Similar challenges arise for other polygons. For example, finding the perimeter of a pentagon, hexagon, or other polygon given only the area requires additional information about the side lengths or relationships between them. The more sides the polygon has, the more complex the equations become.
Limitations and Advanced Techniques
The primary limitation when finding the perimeter given only the area is the ambiguity of the solution. Unless the shape and additional constraints are specified, there's no unique solution. In these cases, we often need to rely on advanced techniques or make certain assumptions.
Optimization Problems
In some situations, we might be interested in finding the perimeter that is either maximized or minimized given a fixed area. These are optimization problems that often require calculus. For example, determining the rectangle with the minimum perimeter for a given area leads to a square (a square is a special case of a rectangle).
Using Inequalities
Geometric inequalities can help establish bounds for the perimeter given the area. For instance, the isoperimetric inequality states that among all shapes with the same area, the circle has the minimum perimeter. This inequality can give us a lower bound for the perimeter.
Practical Applications
Knowing how to find the perimeter from the area, albeit with limitations, finds applications in several areas:
- Engineering: Optimizing material usage in designing structures (e.g., minimizing the perimeter of a container for a given volume).
- Architecture: Determining efficient layouts for buildings or landscapes.
- Computer graphics: Generating shapes with specified area and approximate perimeter.
- Physics: Modeling physical systems where the area and perimeter influence certain properties.
Conclusion
While knowing the area alone isn't enough to definitively determine the perimeter of a geometric shape, understanding the relationship between area and perimeter, combined with additional information or constraints, enables us to solve this problem for many common shapes. This process highlights the importance of precise problem definition and the need for a thorough understanding of geometric principles. The examples and techniques discussed in this guide provide a solid foundation for tackling the challenges associated with finding the perimeter when the area is known. Remember to always consider the limitations of the problem and the potential need for additional information or assumptions to obtain a unique solution.
Latest Posts
Latest Posts
-
How To Find The Mass Of The Excess Reactant
Apr 02, 2025
-
Instantaneous Rate Of Change Vs Average Rate Of Change
Apr 02, 2025
-
How Many D Orbitals Can Be In An Energy Level
Apr 02, 2025
-
Log Base 2 X 2 Graph
Apr 02, 2025
-
X 3 2x 2 5x 6
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about How To Find Perimeter With Area Given . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
