Instantaneous Rate Of Change Vs Average Rate Of Change
listenit
Apr 02, 2025 · 6 min read
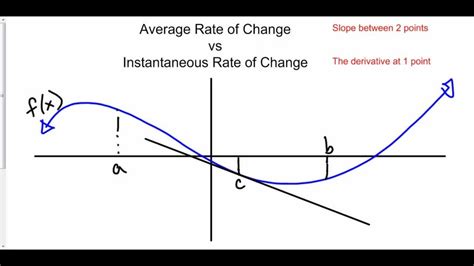
Table of Contents
Instantaneous Rate of Change vs. Average Rate of Change: A Deep Dive
Understanding the rate of change is fundamental in calculus and numerous applications across various fields. While both instantaneous and average rates of change describe how a quantity changes over time or with respect to another variable, they differ significantly in their scope and calculation. This article will delve into the core concepts of each, exploring their differences, applications, and illustrating them with real-world examples.
What is the Average Rate of Change?
The average rate of change measures the overall change of a function over a specific interval. It provides a global perspective, considering the function's behavior across the entire interval, not just at a single point. Imagine driving a car; the average speed calculates the total distance traveled divided by the total time taken. This doesn't tell us anything about your speed at any specific moment but rather your average speed throughout the journey.
Mathematically, the average rate of change of a function f(x) over the interval [a, b] is defined as:
(f(b) - f(a)) / (b - a)
This formula calculates the slope of the secant line connecting the points (a, f(a)) and (b, f(b)) on the graph of the function. The secant line provides a visual representation of the average rate of change.
Example:
Let's consider the function f(x) = x². We want to find the average rate of change between x = 1 and x = 3.
f(1) = 1² = 1 f(3) = 3² = 9
Average rate of change = (9 - 1) / (3 - 1) = 8 / 2 = 4
Therefore, the average rate of change of f(x) = x² between x = 1 and x = 3 is 4. This means that, on average, the function's value increased by 4 units for every unit increase in x over this interval.
What is the Instantaneous Rate of Change?
The instantaneous rate of change, on the other hand, measures the rate of change at a specific point in time or at a particular value of the independent variable. It provides a local perspective, focusing solely on the function's behavior at that precise moment. Returning to the car analogy, the speedometer displays the instantaneous speed – your speed at that very instant.
Mathematically, the instantaneous rate of change is given by the derivative of the function at that point. The derivative represents the slope of the tangent line to the curve at that point. The tangent line touches the curve at only one point, providing a precise measure of the function's rate of change at that instant.
Finding the Instantaneous Rate of Change:
To find the instantaneous rate of change, we need to take the limit as the interval approaches zero. This is formalized by the definition of the derivative:
f'(x) = lim (h→0) [(f(x + h) - f(x)) / h]
where f'(x) denotes the derivative of f(x) with respect to x. The derivative provides a function that gives the instantaneous rate of change at any point x in the domain of f(x).
Example:
Let's use the same function, f(x) = x². To find the instantaneous rate of change at x = 2, we first find the derivative:
f'(x) = 2x
Now, we substitute x = 2 into the derivative:
f'(2) = 2 * 2 = 4
The instantaneous rate of change of f(x) = x² at x = 2 is 4. This signifies that at the precise point x = 2, the function's value is increasing at a rate of 4 units for every unit increase in x.
Key Differences Summarized:
| Feature | Average Rate of Change | Instantaneous Rate of Change |
|---|---|---|
| Scope | Global (over an interval) | Local (at a specific point) |
| Calculation | Slope of the secant line | Slope of the tangent line (derivative) |
| Representation | (f(b) - f(a)) / (b - a) | f'(x) = lim (h→0) [(f(x + h) - f(x)) / h] |
| Interpretation | Average change over the interval | Rate of change at a specific instant |
Real-World Applications:
Both average and instantaneous rates of change have wide-ranging applications in various fields:
Average Rate of Change:
- Physics: Calculating average speed, velocity, or acceleration over a period. For instance, determining the average speed of a vehicle during a road trip.
- Finance: Analyzing average growth of investments over time. For example, calculating the average annual return of a stock over five years.
- Economics: Measuring average production changes, average cost changes, or average revenue over a specific period.
Instantaneous Rate of Change:
- Physics: Determining the exact speed of a vehicle at a particular moment, or calculating the instantaneous acceleration at any given time.
- Engineering: Analyzing the rate of change of temperature in a system, or the rate of fluid flow at a specific point in a pipe.
- Medicine: Measuring the instantaneous rate of drug absorption into the bloodstream.
- Biology: Studying population growth rates at specific times, or the rate of change in the concentration of a chemical within a cell.
Connecting Average and Instantaneous Rates of Change:
While seemingly distinct, the average and instantaneous rates of change are intrinsically linked. The average rate of change over a very small interval provides an approximation of the instantaneous rate of change at a point within that interval. As the interval shrinks towards zero, the average rate of change converges to the instantaneous rate of change. This fundamental connection is at the heart of the concept of the derivative in calculus.
Advanced Concepts and Applications:
Beyond the basics, understanding the nuances of average and instantaneous rates of change opens doors to more advanced concepts:
- Higher-order derivatives: The derivative of a derivative gives the second derivative, representing the rate of change of the rate of change (like acceleration being the derivative of velocity).
- Optimization problems: Finding maximum and minimum values of functions often involves analyzing the instantaneous rate of change (derivative) to identify critical points.
- Differential equations: These equations relate a function to its derivatives, modelling dynamic systems across various disciplines, from physics and engineering to biology and economics.
- Machine learning: Gradient descent, a fundamental algorithm in machine learning, relies on calculating instantaneous rates of change (gradients) to optimize model parameters.
Conclusion:
The distinction between average and instantaneous rates of change is crucial for a thorough understanding of calculus and its practical applications. While the average rate of change provides a global overview of a function's behavior over an interval, the instantaneous rate of change offers a precise local measure at a specific point. Both concepts are essential tools for analyzing change in various contexts, from everyday phenomena to complex scientific models. Mastering these concepts is a key step in developing a strong foundation in mathematics and its applications in numerous fields. By understanding these differences and their interconnectedness, one can effectively analyze and model dynamic systems and draw meaningful insights from the data.
Latest Posts
Latest Posts
-
Reacts With Water Chemical Or Physical
Apr 03, 2025
-
How Many Cups In Two Gallons
Apr 03, 2025
-
Isotopes Are Atoms Of The Same Element That Have
Apr 03, 2025
-
Is A Dog A Person Place Or Thing
Apr 03, 2025
-
What Is The Fraction Of 78
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Instantaneous Rate Of Change Vs Average Rate Of Change . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
