X 3 2x 2 5x 6
listenit
Apr 02, 2025 · 5 min read
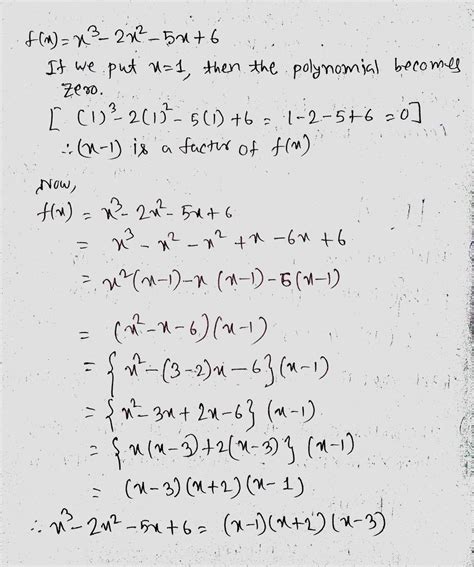
Table of Contents
Deconstructing the Expression: x³ + 2x² + 5x + 6
This seemingly simple algebraic expression, x³ + 2x² + 5x + 6, offers a rich landscape for exploration. It's a cubic polynomial, meaning its highest power of x is 3. While it might appear straightforward at first glance, understanding its properties, potential applications, and methods of manipulation opens doors to a deeper comprehension of algebra and its broader implications in mathematics and beyond. This article will delve into the intricacies of this expression, examining its factorization, potential roots, graphing techniques, and practical applications.
Understanding Cubic Polynomials
Before we dissect x³ + 2x² + 5x + 6 specifically, let's establish a foundational understanding of cubic polynomials. A cubic polynomial is a polynomial of degree three, meaning the highest power of the variable (in this case, x) is 3. The general form is:
ax³ + bx² + cx + d
where 'a', 'b', 'c', and 'd' are constants, and 'a' is not equal to zero (otherwise it wouldn't be a cubic polynomial). Our specific expression, x³ + 2x² + 5x + 6, fits this form perfectly with a=1, b=2, c=5, and d=6.
Key Properties of Cubic Polynomials
- At most three real roots: A cubic polynomial can have up to three real roots (values of x that make the polynomial equal to zero). It can also have complex roots (involving the imaginary unit 'i').
- One or three real roots: Cubic polynomials always have at least one real root. This is a consequence of the Intermediate Value Theorem.
- Possible shapes: The graph of a cubic polynomial is a curve with a characteristic 'S' shape. It can have two turning points (local maxima and minima), one turning point, or no turning points depending on the values of its coefficients.
Factorization of x³ + 2x² + 5x + 6
Factorization is a crucial step in understanding the behavior of a polynomial. It involves expressing the polynomial as a product of simpler factors. For our expression, x³ + 2x² + 5x + 6, finding factors can be approached using several methods.
Rational Root Theorem
One powerful technique is the Rational Root Theorem. This theorem states that any rational root (a root that can be expressed as a fraction p/q, where p is a factor of the constant term and q is a factor of the leading coefficient) of a polynomial must be of this form.
In our case:
- The constant term is 6 (factors: ±1, ±2, ±3, ±6)
- The leading coefficient is 1 (factors: ±1)
Therefore, potential rational roots are ±1, ±2, ±3, and ±6. We can test these values by substituting them into the expression:
- f(1) = 1³ + 2(1)² + 5(1) + 6 = 14 ≠ 0
- f(-1) = (-1)³ + 2(-1)² + 5(-1) + 6 = 2 ≠ 0
- f(2) = 2³ + 2(2)² + 5(2) + 6 = 26 ≠ 0
- f(-2) = (-2)³ + 2(-2)² + 5(-2) + 6 = -4 ≠ 0
- f(3) = 3³ + 2(3)² + 5(3) + 6 = 54 ≠ 0
- f(-3) = (-3)³ + 2(-3)² + 5(-3) + 6 = 0
We found that x = -3 is a root! This means (x + 3) is a factor.
Polynomial Long Division
Now that we have one factor, we can use polynomial long division to find the remaining factors. Dividing x³ + 2x² + 5x + 6 by (x + 3) gives us:
x² - x + 2
Therefore, the complete factorization is:
(x + 3)(x² - x + 2)
This quadratic factor, x² - x + 2, cannot be further factored using real numbers. To find its roots, we would need to use the quadratic formula, which would result in complex roots.
Graphing the Cubic Polynomial
Visualizing the polynomial through graphing provides valuable insights into its behavior. The graph will reveal the roots (x-intercepts), turning points, and the overall shape of the function.
Key Features of the Graph
- x-intercept at x = -3: This corresponds to the real root we found through factorization.
- No other x-intercepts: The quadratic factor x² - x + 2 has no real roots, meaning the graph doesn't intersect the x-axis again.
- One turning point: Because the quadratic factor has no real roots and the coefficient of the cubic term is positive, the graph will have a single turning point (a local minimum).
Plotting points and sketching the curve based on these features will give a clear representation of the polynomial's behavior. Software like Desmos or GeoGebra can be used for accurate plotting.
Applications of Cubic Polynomials
Cubic polynomials have numerous applications across various fields:
Engineering and Physics
- Modeling projectile motion: The trajectory of a projectile under the influence of gravity can be modeled using a cubic polynomial.
- Fluid dynamics: Cubic polynomials are used to describe the flow of fluids in certain situations.
- Mechanical engineering: They find applications in modeling the displacement, velocity, and acceleration of mechanical systems.
Economics and Finance
- Modeling economic growth: Cubic polynomials can be used to model economic growth over time, accounting for fluctuations and turning points.
- Financial modeling: They can be employed in certain types of financial modeling and forecasting.
Other Applications
- Computer graphics: Cubic polynomials are crucial in creating smooth curves and surfaces in computer-aided design and computer graphics.
- Data fitting: They can be used to fit curves to data points, providing a mathematical representation of observed trends.
Conclusion
The seemingly simple expression x³ + 2x² + 5x + 6 offers a rich tapestry of mathematical concepts. By exploring its factorization, determining its roots (both real and complex), graphing its behavior, and examining its practical applications, we gain a deeper appreciation for the power and versatility of cubic polynomials. The methods outlined here – the Rational Root Theorem, polynomial long division, and graphical analysis – provide a strong foundation for tackling similar algebraic expressions and understanding the broader world of polynomial functions. Further exploration into the intricacies of cubic polynomials can lead to a deeper understanding of advanced mathematical concepts and their numerous practical applications in diverse fields. Understanding these fundamental mathematical principles allows for more effective problem-solving and a stronger ability to model real-world phenomena.
Latest Posts
Latest Posts
-
Isotopes Are Atoms Of The Same Element That Have
Apr 03, 2025
-
Is A Dog A Person Place Or Thing
Apr 03, 2025
-
What Is The Fraction Of 78
Apr 03, 2025
-
What Is A Reactant Of Photosynthesis
Apr 03, 2025
-
What Happens To Water Molecules In Light Reactions
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about X 3 2x 2 5x 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
