Log Base 2 X 2 Graph
listenit
Apr 02, 2025 · 6 min read
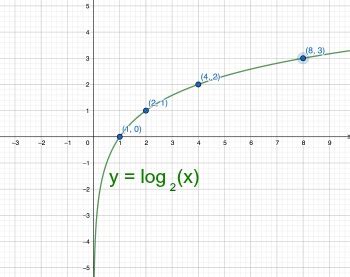
Table of Contents
Log Base 2 x + 2 Graph: A Deep Dive into its Properties and Applications
The logarithmic function, specifically the logarithm base 2, plays a crucial role in various fields, from computer science and information theory to finance and engineering. Understanding its graphical representation, particularly the graph of log₂(x + 2), is key to grasping its behavior and applications. This article will comprehensively explore the graph of log₂(x + 2), analyzing its key features, transformations, asymptotes, domain and range, and providing practical examples of its use.
Understanding the Parent Function: log₂x
Before delving into log₂(x + 2), it's essential to understand the parent function, log₂x. This function represents the exponent to which 2 must be raised to obtain x.
-
Key Features of log₂x:
- Domain: (0, ∞). The logarithm of a non-positive number is undefined in the real number system.
- Range: (-∞, ∞). Logarithmic functions have an unbounded range.
- x-intercept: (1, 0). This is because log₂(1) = 0.
- Vertical Asymptote: x = 0. The function approaches negative infinity as x approaches 0 from the right.
- Increasing Function: The function is strictly increasing; as x increases, so does log₂x.
- No Horizontal Asymptote: The function does not approach a specific value as x tends to infinity.
Transformations: From log₂x to log₂(x + 2)
The graph of log₂(x + 2) is a transformation of the parent function log₂x. Specifically, it involves a horizontal shift. The "+2" inside the logarithm argument indicates a horizontal shift of 2 units to the left.
- Effect of the Horizontal Shift: Every point (x, y) on the graph of log₂x is shifted to (x - 2, y) on the graph of log₂(x + 2). This means the entire graph moves 2 units to the left.
Analyzing the Graph of log₂(x + 2):
Considering the transformation, we can now describe the key features of the graph of log₂(x + 2):
- Domain: (-2, ∞). The argument of the logarithm, x + 2, must be greater than 0, so x > -2.
- Range: (-∞, ∞). The range remains unchanged from the parent function.
- x-intercept: (-1, 0). This is found by solving log₂(x + 2) = 0, which implies x + 2 = 1, thus x = -1.
- Vertical Asymptote: x = -2. The function approaches negative infinity as x approaches -2 from the right.
- Increasing Function: Like the parent function, log₂(x + 2) is also a strictly increasing function.
- No Horizontal Asymptote: The function's behavior at infinity remains unchanged.
Visualizing the Graph:
Imagine the graph of log₂x. Now, shift this entire graph 2 units to the left. The vertical asymptote, initially at x = 0, now moves to x = -2. The x-intercept, initially at (1, 0), now shifts to (-1, 0). The overall shape and behavior of the curve remain similar, only its position on the coordinate plane is altered.
Practical Applications:
The logarithmic function, particularly with base 2, finds widespread applications in various fields. Here are some examples where the understanding of the graph of log₂(x + 2) can be beneficial:
-
Computer Science: Log base 2 is frequently used in computer science to represent the number of bits required to represent a number. For example, log₂(n) represents the number of bits needed to represent an integer n. A modified version, like log₂(x + 2), could represent a scenario where a base level of 2 bits is always present, regardless of the input. This could model scenarios involving data overhead or initial fixed data storage.
-
Information Theory: In information theory, logarithms base 2 are used to calculate information content and entropy. The graph can help visualize how the information content changes with the addition of a constant factor, represented by the "+2".
-
Finance: Logarithmic scales are often used to represent financial data, particularly when dealing with large ranges of values. The graph of log₂(x + 2) could model situations where a minimum base value is involved before logarithmic growth is observed. For example, consider a model for company growth where a certain minimum level of investment is always required.
-
Signal Processing: Logarithmic functions are used in signal processing for amplitude scaling and analysis. The addition of a constant could represent a baseline signal level that’s always present.
-
Chemistry: The study of reaction rates often uses logarithmic scales. The graph may be applied to model situations where an initial catalyst is involved affecting reaction rates.
Comparing log₂(x) and log₂(x+2): A Tabular Representation
To further illustrate the transformation, let's compare some values of log₂(x) and log₂(x + 2):
| x | log₂(x) | x + 2 | log₂(x + 2) |
|---|---|---|---|
| 0.5 | -1 | 2.5 | ≈ 1.32 |
| 1 | 0 | 3 | ≈ 1.58 |
| 2 | 1 | 4 | 2 |
| 4 | 2 | 6 | ≈ 2.58 |
| 8 | 3 | 10 | ≈ 3.32 |
| 16 | 4 | 18 | ≈ 4.17 |
The table clearly shows that for each x value, the corresponding log₂(x + 2) value is greater, reflecting the leftward shift of the graph.
Advanced Concepts and Extensions:
-
Derivatives and Integrals: Understanding the derivative and integral of log₂(x + 2) allows for further analysis of its behavior, such as finding slopes and areas under the curve.
-
Series Expansions: The function can be approximated using Taylor or Maclaurin series, particularly useful for numerical computations.
-
Inverse Function: The inverse function of log₂(x + 2) is 2ˣ - 2. Graphing this alongside log₂(x + 2) provides valuable insights into their relationship.
-
Multiple Transformations: Exploring the effects of other transformations, such as vertical shifts, stretches, and reflections, on the graph of log₂(x + 2) provides a deeper understanding of function transformations in general.
-
Solving Equations involving log₂(x + 2): Using the properties of logarithms, you can solve various equations and inequalities involving this function, deepening your understanding of its applications.
Conclusion:
The graph of log₂(x + 2) represents a fundamental concept in mathematics with far-reaching implications across various scientific and engineering disciplines. Understanding its properties – its domain and range, asymptotes, transformations from the parent function, and its increasing nature – is crucial for effectively applying it in problem-solving and model-building. Its applications span from analyzing data in computer science and information theory to modeling growth in finance and studying rates of reaction in chemistry. This comprehensive exploration, through both graphical representation and numerical examples, aims to provide a strong foundation for anyone interested in leveraging the power of logarithmic functions, particularly log₂(x + 2), in their respective fields. Remember to always carefully consider the domain and range when working with logarithmic functions to avoid errors and ensure accurate interpretations.
Latest Posts
Latest Posts
-
Is A Dog A Person Place Or Thing
Apr 03, 2025
-
What Is The Fraction Of 78
Apr 03, 2025
-
What Is A Reactant Of Photosynthesis
Apr 03, 2025
-
What Happens To Water Molecules In Light Reactions
Apr 03, 2025
-
9 6 4u 1 U 15
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Log Base 2 X 2 Graph . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
