How Many D Orbitals Can Be In An Energy Level
listenit
Apr 02, 2025 · 6 min read
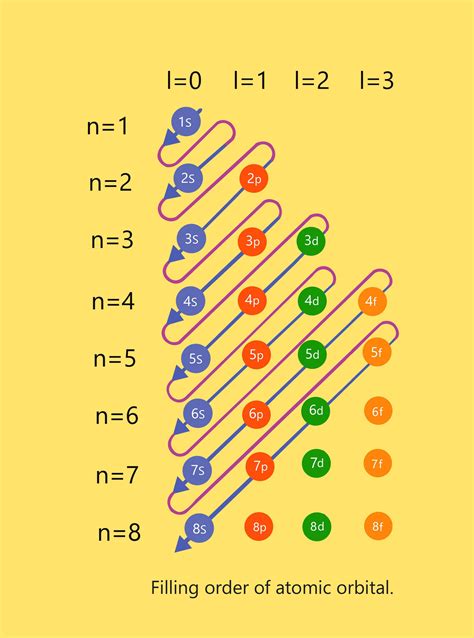
Table of Contents
How Many d Orbitals Can Be in an Energy Level? Unveiling the Mysteries of Atomic Orbitals
Understanding the intricacies of atomic structure is crucial for comprehending the behavior of matter. A key component of this understanding lies in grasping the concept of atomic orbitals, particularly the d orbitals and their distribution within energy levels. This article delves deep into the quantum mechanics behind d orbitals, explaining how many can exist within a given energy level and why. We will explore the nuances of electron configuration, quantum numbers, and the spatial distribution of these orbitals to provide a comprehensive answer.
The Quantum Mechanical Model: The Foundation of Atomic Orbitals
Before we jump into the specifics of d orbitals, it's vital to understand the framework within which they exist: the quantum mechanical model of the atom. This model employs quantum numbers to describe the properties of electrons and their orbitals. These numbers are not arbitrary; they arise directly from the solutions to the Schrödinger equation, a cornerstone of quantum mechanics.
The Four Quantum Numbers: Defining an Electron's State
Four quantum numbers define the state of an electron within an atom:
-
Principal Quantum Number (n): This integer (n = 1, 2, 3...) dictates the energy level and the average distance of the electron from the nucleus. Higher n values correspond to higher energy levels and greater distances.
-
Azimuthal Quantum Number (l): This integer (l = 0, 1, 2... n-1) determines the shape of the orbital and its angular momentum. It also specifies the subshell: l = 0 (s subshell), l = 1 (p subshell), l = 2 (d subshell), l = 3 (f subshell), and so on.
-
Magnetic Quantum Number (ml): This integer (ml = -l, -l+1,... 0,... l-1, l) describes the orientation of the orbital in space. For example, a p subshell (l=1) has three possible orientations (ml = -1, 0, 1), corresponding to the px, py, and pz orbitals.
-
Spin Quantum Number (ms): This number (ms = +1/2 or -1/2) describes the intrinsic angular momentum (spin) of the electron. Each orbital can hold a maximum of two electrons, one with spin up (+1/2) and one with spin down (-1/2), according to the Pauli Exclusion Principle.
The d Orbitals: Shape, Orientation, and Energy
The d orbitals are characterized by the azimuthal quantum number l = 2. This means that within a given energy level (n), d orbitals will exist if and only if n ≥ 3. Why? Because l cannot be greater than or equal to n.
The five d orbitals within a subshell have distinct shapes and orientations:
-
dz²: This orbital has a dumbbell shape along the z-axis, with a toroidal ring in the xy-plane.
-
dx² - y²: This orbital has a dumbbell shape along the x and y axes, with lobes pointing along the x and y axes.
-
dxy: This orbital has four lobes lying in the xy plane, between the x and y axes.
-
dxz: This orbital has four lobes lying in the xz plane, between the x and z axes.
-
dyz: This orbital has four lobes lying in the yz plane, between the y and z axes.
These five d orbitals are all degenerate (have the same energy) in an isolated atom, but this degeneracy can be lifted in the presence of ligands in coordination complexes, leading to phenomena like crystal field splitting.
How Many d Orbitals Per Energy Level?
The number of d orbitals in a given energy level is directly determined by the number of possible values for the magnetic quantum number (ml) when l = 2. Since ml can range from -l to +l, including zero, there are 2l + 1 possible values. For d orbitals (l = 2), this means there are 2(2) + 1 = 5 d orbitals.
Therefore, regardless of the principal quantum number (n), there are always five d orbitals within a given energy level, provided that n ≥ 3.
Energy Levels and the Presence of d Orbitals: A Detailed Look
Let's examine this in the context of specific energy levels:
-
n = 1: No d orbitals exist because the maximum value of l is n-1 = 0, corresponding to the s subshell.
-
n = 2: No d orbitals exist; the maximum value of l is n-1 = 1, corresponding to the p subshell.
-
n = 3: Five d orbitals exist (3d subshell).
-
n = 4: Five d orbitals exist (4d subshell).
-
n = 5: Five d orbitals exist (5d subshell).
And so on. The pattern is clear: once n reaches 3 or higher, five d orbitals become available, always maintaining their characteristic shapes and spatial orientations, though their energies will vary depending on the atomic number and surrounding environment.
The Significance of d Orbitals: Implications in Chemistry and Physics
The presence and properties of d orbitals are paramount to many chemical and physical phenomena. Their involvement extends across diverse areas:
-
Transition Metal Chemistry: Transition metals are characterized by partially filled d orbitals, which are central to their distinctive properties such as variable oxidation states, colorful complexes, and catalytic activity. The ability of d orbitals to participate in bonding explains the intricate coordination chemistry of transition metal compounds.
-
Spectroscopy: The electronic transitions involving d orbitals are responsible for the characteristic colors of many transition metal complexes. Spectroscopic techniques are vital in probing the electronic structure and geometry of these compounds.
-
Materials Science: d orbitals play a significant role in the properties of many materials, influencing conductivity, magnetism, and catalytic behavior. Understanding the electronic configuration and interactions involving d orbitals is crucial for designing novel materials with tailored properties.
-
Catalysis: The ability of transition metals to facilitate chemical reactions is often linked to their d orbitals. Many catalysts contain transition metals that utilize d orbitals for binding reactants and facilitating the reaction pathway.
Conclusion: A Comprehensive Understanding of d Orbitals
In conclusion, the number of d orbitals that can exist in a given energy level is always five, provided the principal quantum number (n) is 3 or greater. This arises directly from the quantum mechanical model and the constraints on the quantum numbers. The properties and behavior of d orbitals are fundamental to a wide range of phenomena in chemistry, physics, and materials science. Understanding their spatial distribution, energy levels, and involvement in chemical bonding is essential for appreciating the richness and complexity of the atomic world. This knowledge serves as a cornerstone for deeper explorations into the fascinating world of quantum mechanics and its implications across scientific disciplines. The consistent presence of five d orbitals within any energy level beyond n=2 highlights the elegance and predictability of the quantum mechanical model in describing the structure of atoms.
Latest Posts
Latest Posts
-
Reacts With Water Chemical Or Physical
Apr 03, 2025
-
How Many Cups In Two Gallons
Apr 03, 2025
-
Isotopes Are Atoms Of The Same Element That Have
Apr 03, 2025
-
Is A Dog A Person Place Or Thing
Apr 03, 2025
-
What Is The Fraction Of 78
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about How Many D Orbitals Can Be In An Energy Level . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
