How Many Lines Of Symmetry Does A Regular Decagon Have
listenit
Mar 30, 2025 · 5 min read
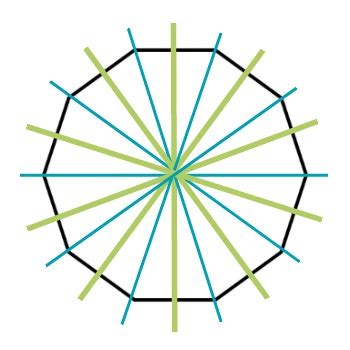
Table of Contents
How Many Lines of Symmetry Does a Regular Decagon Have? A Comprehensive Exploration
A regular decagon, a captivating geometric shape, holds a unique place in the world of geometry. Understanding its properties, especially its lines of symmetry, opens doors to a deeper appreciation of its inherent beauty and mathematical elegance. This article delves into the fascinating question: How many lines of symmetry does a regular decagon have? We'll not only answer this question but also explore the underlying concepts of symmetry, delve into the characteristics of regular polygons, and examine the symmetry of other polygons for comparison.
Understanding Lines of Symmetry
Before we tackle the decagon, let's establish a solid understanding of what a line of symmetry is. A line of symmetry, also known as a reflectional symmetry or a mirror line, is a line that divides a shape into two identical halves that are mirror images of each other. If you were to fold the shape along this line, the two halves would perfectly overlap.
Think of a simple example: a square. A square possesses four lines of symmetry – two that connect opposite corners (diagonal lines) and two that connect the midpoints of opposite sides (vertical and horizontal lines). These lines effectively divide the square into two congruent halves.
Properties of Regular Polygons
Regular polygons are characterized by their equal sides and equal angles. This uniformity plays a crucial role in determining their lines of symmetry. The number of sides directly impacts the number of lines of symmetry. Let's look at some examples:
- Equilateral Triangle: Three lines of symmetry (each line connects a vertex to the midpoint of the opposite side).
- Square: Four lines of symmetry (two diagonals and two lines connecting midpoints of opposite sides).
- Regular Pentagon: Five lines of symmetry (each line connects a vertex to the midpoint of the opposite side).
- Regular Hexagon: Six lines of symmetry (three lines connecting opposite vertices and three lines connecting midpoints of opposite sides).
Notice a pattern emerging? The number of lines of symmetry in a regular polygon is equal to the number of its sides. This holds true for all regular polygons.
Determining the Lines of Symmetry in a Regular Decagon
Now, let's focus on the star of our show: the regular decagon. A regular decagon is a ten-sided polygon with all sides and angles equal. Following the pattern observed in other regular polygons, we can deduce the number of lines of symmetry.
Answer: A regular decagon has ten lines of symmetry.
These lines of symmetry are of two types:
- Five lines connecting opposite vertices: These lines pass through the center of the decagon and connect opposite vertices, effectively dividing it into two congruent pentagons.
- Five lines connecting midpoints of opposite sides: These lines also pass through the center and connect the midpoints of opposite sides, again dividing the decagon into two congruent halves.
Each of these ten lines perfectly bisects the decagon, creating two mirror-image halves. This symmetrical nature is a key characteristic that contributes to the decagon's aesthetic appeal.
Visualizing the Lines of Symmetry
Imagine a regular decagon drawn on a piece of paper. To visualize the lines of symmetry, try the following:
- Draw lines connecting opposite vertices: You'll notice five such lines, each dividing the decagon into two congruent parts.
- Draw lines connecting the midpoints of opposite sides: Again, you'll find five lines, each creating a perfect reflection.
- Fold the paper: Fold the paper along each of these ten lines. If the two halves perfectly overlap, you've successfully identified a line of symmetry.
This hands-on approach can provide a clearer understanding of the decagon's symmetrical properties.
Symmetry in Other Polygons: A Comparative Analysis
Let's broaden our perspective by comparing the symmetry of a regular decagon with other polygons:
| Polygon | Number of Sides | Number of Lines of Symmetry |
|---|---|---|
| Equilateral Triangle | 3 | 3 |
| Square | 4 | 4 |
| Regular Pentagon | 5 | 5 |
| Regular Hexagon | 6 | 6 |
| Regular Heptagon | 7 | 7 |
| Regular Octagon | 8 | 8 |
| Regular Nonagon | 9 | 9 |
| Regular Decagon | 10 | 10 |
| Regular Dodecagon | 12 | 12 |
This table clearly shows the direct correlation between the number of sides and the number of lines of symmetry in regular polygons.
Beyond Lines of Symmetry: Rotational Symmetry
Regular polygons also exhibit rotational symmetry. Rotational symmetry refers to the ability of a shape to be rotated about a central point and still appear unchanged. A regular decagon has rotational symmetry of order 10, meaning it can be rotated 36 degrees (360/10) ten times before returning to its original orientation. This rotational symmetry, combined with its reflectional symmetry, contributes to its overall symmetry and balanced appearance.
Applications of Decagonal Symmetry
The symmetrical properties of a decagon, like other regular polygons, find applications in various fields:
- Architecture: Decagonal structures can be aesthetically pleasing and structurally sound.
- Design: The symmetrical nature of a decagon is often utilized in creating logos, patterns, and artwork.
- Nature: Although less common than other polygons, decagonal shapes can be found in some naturally occurring structures.
- Mathematics: The study of decagons and their symmetry contributes to a broader understanding of geometry and mathematical concepts.
Conclusion: The Elegant Symmetry of the Decagon
The regular decagon, with its ten lines of symmetry, stands as a testament to the beauty and order found within geometric shapes. Its symmetrical properties, both reflectional and rotational, make it a fascinating subject for mathematical exploration and a visually appealing element in design and architecture. Understanding the principles of symmetry, as demonstrated through the decagon, provides a deeper appreciation for the underlying order and elegance present in the world around us. By grasping the fundamental concepts of symmetry and applying them to regular polygons, we can unlock a whole new level of appreciation for the mathematical world and its aesthetic manifestations. The seemingly simple question, "How many lines of symmetry does a regular decagon have?" opens the door to a deeper understanding of geometric principles and their diverse applications.
Latest Posts
Latest Posts
-
What Is The Area Of This Circle In Square Centimeters
Apr 01, 2025
-
What Is The Improper Fraction Of 2 1 4
Apr 01, 2025
-
Lewis Acid Vs Bronsted Lowry Acid
Apr 01, 2025
-
What Is Square Root Of 63
Apr 01, 2025
-
Least Common Multiple 2 And 4
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about How Many Lines Of Symmetry Does A Regular Decagon Have . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
