What Is Square Root Of 63
listenit
Apr 01, 2025 · 5 min read
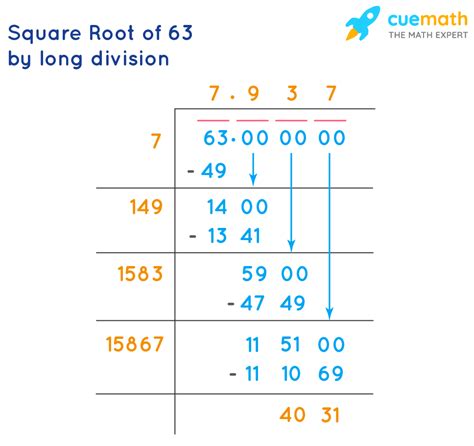
Table of Contents
What is the Square Root of 63? A Deep Dive into Square Roots and Their Applications
The question, "What is the square root of 63?" might seem simple at first glance. A quick calculation on a calculator will give you a decimal approximation. However, exploring this seemingly straightforward question opens up a fascinating world of mathematical concepts, their historical development, and their practical applications in various fields. This article delves deep into understanding square roots, specifically the square root of 63, examining its properties, calculation methods, and real-world relevance.
Understanding Square Roots
Before we tackle the square root of 63 specifically, let's establish a foundational understanding of square roots. A square root of a number is a value that, when multiplied by itself (squared), gives the original number. For example, the square root of 9 is 3 because 3 x 3 = 9. This can be represented mathematically as √9 = 3.
The concept of square roots is intimately connected to the concept of squaring a number. Squaring a number involves multiplying it by itself. For instance, 5 squared (5²) is 25 (5 x 5 = 25). The square root is simply the inverse operation of squaring.
Perfect Squares and Non-Perfect Squares
Numbers that have whole number square roots are called perfect squares. Examples include 4 (√4 = 2), 9 (√9 = 3), 16 (√16 = 4), and so on. 63, however, is not a perfect square. This means its square root is not a whole number. Numbers like 63, whose square roots are not whole numbers, are known as non-perfect squares.
Calculating the Square Root of 63
Since 63 is a non-perfect square, its square root will be an irrational number – a number that cannot be expressed as a simple fraction and has an infinite, non-repeating decimal expansion.
Method 1: Using a Calculator
The simplest way to find an approximation of the square root of 63 is to use a calculator. Most calculators have a square root function (√). Simply enter 63 and press the square root button. You'll get a result approximately equal to 7.93725.
Method 2: Estimation and Approximation
Even without a calculator, we can estimate the square root of 63. We know that 8² = 64, which is very close to 63. Therefore, we can reasonably estimate that the square root of 63 is slightly less than 8. This method provides a rough approximation, useful for quick mental calculations.
Method 3: Babylonian Method (Hero's Method)
A more sophisticated method for approximating square roots is the Babylonian method, also known as Heron's method. This iterative method refines an initial guess to obtain progressively closer approximations.
Here's how it works for √63:
- Make an initial guess: Let's start with 8 (since 8² = 64).
- Improve the guess: Divide the number (63) by the guess (8): 63 / 8 = 7.875
- Average: Average the result from step 2 and the original guess: (8 + 7.875) / 2 = 7.9375
- Repeat: Repeat steps 2 and 3 using the new average as the guess. The more iterations you perform, the closer you get to the actual square root.
This method, while more complex than using a calculator, demonstrates a powerful algorithm for approximating square roots, showcasing fundamental mathematical principles.
Method 4: Prime Factorization and Simplification
While we can't simplify √63 to a whole number, we can simplify it using prime factorization. The prime factorization of 63 is 3² x 7. Therefore, √63 can be expressed as √(3² x 7) = √3² x √7 = 3√7. This form is often preferred in mathematical contexts because it represents the square root in its simplest radical form. This shows that 3 multiplied by the square root of 7 will result in the square root of 63.
Applications of Square Roots
Square roots are not just abstract mathematical concepts; they have numerous applications in various fields:
Geometry and Trigonometry
Square roots are fundamental to many geometric calculations. For example:
- Calculating the hypotenuse of a right-angled triangle: The Pythagorean theorem (a² + b² = c²) utilizes square roots to find the length of the hypotenuse (c) given the lengths of the other two sides (a and b).
- Finding the area of a square: The side length of a square is the square root of its area.
- Calculating distances: Many distance formulas in coordinate geometry involve square roots.
Physics and Engineering
Square roots frequently appear in physics and engineering formulas:
- Calculating velocity: Formulas involving velocity often use square roots.
- Calculating energy: Energy calculations can involve square roots, particularly in physics problems dealing with kinetic energy and potential energy.
- Civil engineering: Determining the structural integrity of buildings and bridges requires calculations using square roots.
Statistics and Probability
Square roots play a significant role in statistics:
- Standard deviation: The standard deviation of a dataset, a measure of data dispersion, involves square roots.
- Error analysis: Calculations of experimental errors often involve square roots.
Computer Graphics and Game Development
Square roots are essential for calculations in computer graphics and game development:
- Distance calculations: Determining the distance between objects on a screen frequently involves the Pythagorean theorem and square roots.
- Vector calculations: Vector operations, crucial for representing objects and their movement in 3D space, often utilize square roots.
Finance and Economics
Square roots are used in financial calculations:
- Standard deviation of investment returns: This is a crucial metric for assessing risk in portfolio management.
- Option pricing models: Some sophisticated options pricing models involve square roots in their formulas.
Conclusion
While the answer to "What is the square root of 63?" is approximately 7.93725, or more precisely 3√7, the question's significance extends far beyond a simple numerical result. Understanding square roots reveals a fundamental aspect of mathematics with broad applications across diverse fields. From calculating distances in geometry to analyzing financial data, square roots are an indispensable tool in our understanding and interaction with the world. This exploration has hopefully provided a more comprehensive appreciation of this seemingly simple yet remarkably important mathematical concept. Further exploration into advanced mathematical concepts like complex numbers and higher-order roots will reveal even deeper applications and intricacies related to the broader theme of square roots and their importance in problem-solving.
Latest Posts
Latest Posts
-
Irrational Numbers Between 1 And 6
Apr 02, 2025
-
In A Hypertonic Solution A Cell Will
Apr 02, 2025
-
How Many Kilograms Are In 5000 Grams
Apr 02, 2025
-
Solve This Inequality 3b 7 32
Apr 02, 2025
-
Number Of Valence Electrons In Ar
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is Square Root Of 63 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
