Irrational Numbers Between 1 And 6
listenit
Apr 02, 2025 · 6 min read
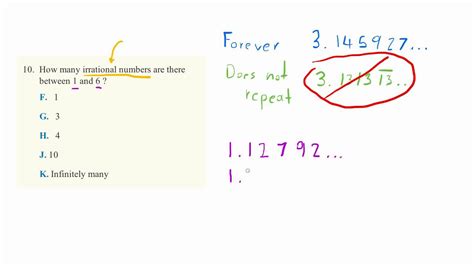
Table of Contents
Irrational Numbers Between 1 and 6: A Deep Dive
The world of numbers extends far beyond the familiar realm of integers and rational numbers. Nestled between these neatly categorized quantities lie the irrational numbers, numbers that cannot be expressed as a simple fraction of two integers. This article delves into the fascinating world of irrational numbers specifically those residing between 1 and 6, exploring their properties, examples, and the significance of their existence within mathematics.
Understanding Irrational Numbers
Before we embark on our journey through the irrational numbers between 1 and 6, let's establish a firm understanding of what defines an irrational number. Simply put, an irrational number is a real number that cannot be expressed as a ratio of two integers (a fraction). This means its decimal representation neither terminates (ends) nor repeats in a predictable pattern. This contrasts sharply with rational numbers, like 1/2 (0.5), 2/3 (0.666...), or 7/4 (1.75), which either have a finite decimal expansion or a repeating decimal expansion.
Key characteristics of irrational numbers:
- Non-terminating decimal expansions: Their decimal representations go on forever without repeating.
- Non-repeating decimal expansions: There's no pattern in the sequence of digits.
- Cannot be expressed as a fraction: They cannot be written as a/b, where 'a' and 'b' are integers and 'b' is not zero.
Famous Irrational Numbers Between 1 and 6
Several well-known irrational numbers fall within the interval (1, 6). Let's explore some prominent examples:
1. √2 (approximately 1.414)
The square root of 2 is perhaps the most famous irrational number. It's the length of the diagonal of a square with sides of length 1, a fact easily proven using the Pythagorean theorem. Its decimal expansion is infinite and non-repeating, beginning 1.41421356...
Why is √2 irrational? This is a classic proof by contradiction. Assume √2 is rational, meaning it can be expressed as a/b, where a and b are integers with no common factors (the fraction is in its simplest form). Squaring both sides gives 2 = a²/b². This implies that a² is an even number (divisible by 2), and therefore 'a' must also be even. If 'a' is even, it can be written as 2k, where k is an integer. Substituting this back into the equation, we get 2 = (2k)²/b², which simplifies to 2b² = 4k². Dividing by 2 gives b² = 2k², showing that b² is also even, and therefore 'b' must be even. This contradicts our initial assumption that a and b have no common factors (they are both even). Therefore, our initial assumption that √2 is rational must be false, proving that √2 is irrational.
2. √3 (approximately 1.732)
Similar to √2, the square root of 3 is another well-known irrational number. It represents the length of the diagonal of a rectangle with sides of length 1 and √2. Its decimal expansion is also infinite and non-repeating, starting with 1.7320508... A similar proof by contradiction can be used to demonstrate its irrationality.
3. √5 (approximately 2.236)
The square root of 5 is yet another example, frequently encountered in geometry and algebra. Its decimal representation is non-terminating and non-repeating, starting 2.2360679... Again, its irrationality can be proven using a similar method as √2 and √3.
4. √6 (approximately 2.449)
The square root of 6 finds applications in various mathematical contexts. Being the square root of a non-perfect square, it's inherently irrational, with a non-terminating and non-repeating decimal expansion: 2.4494897...
5. π (approximately 3.14159)
The famous mathematical constant π (pi), representing the ratio of a circle's circumference to its diameter, is an irrational number. Its infinite and non-repeating decimal expansion is well-known, starting with 3.1415926535... The irrationality of π has been rigorously proven, although the proof is quite complex.
6. e (approximately 2.71828)
Euler's number, denoted by 'e', is another significant irrational number. It's the base of the natural logarithm and appears frequently in calculus and exponential functions. Its decimal expansion, beginning 2.7182818284..., is infinite and non-repeating. The proof of its irrationality also involves advanced mathematical concepts.
7. The Golden Ratio (φ - approximately 1.618)
The Golden Ratio, often represented by the Greek letter phi (φ), is an irrational number approximately equal to 1.6180339887... It's defined as (1 + √5)/2. This ratio appears frequently in nature, art, and architecture, due to its aesthetically pleasing proportions. Its irrationality stems directly from the irrationality of √5.
Generating Irrational Numbers Between 1 and 6
While we've discussed several known irrational numbers, the number of irrational numbers between 1 and 6 is infinite. Here are some methods to generate more:
- Square roots of non-perfect squares: Any non-perfect square between 1 and 36 (6²) will yield an irrational square root within our desired range. For instance, √7, √8, √10, √11, √12, and so on, all fall between 1 and 6 and are irrational.
- Cube roots, fourth roots, etc.: Similar to square roots, taking the nth root (where n is an integer greater than 1) of any non-perfect nth power within the range will often produce an irrational number.
- Sums and differences: Adding or subtracting rational and irrational numbers (keeping the result within the range) typically results in an irrational number. For instance, 2 + √2 is irrational and falls between 1 and 6.
- Transcendental numbers: Transcendental numbers are a subset of irrational numbers that are not roots of any polynomial equation with rational coefficients. Numbers like π and e are examples. There are many other transcendental numbers, but identifying them can be far more complex.
The Significance of Irrational Numbers
The existence of irrational numbers might seem like a mathematical curiosity, but they are fundamental to many areas of mathematics and science:
- Geometry: Irrational numbers are essential in geometry, appearing in calculations involving circles (π), triangles, and other shapes. The Pythagorean theorem often leads to irrational lengths.
- Calculus: Irrational numbers are crucial in calculus, particularly in dealing with limits, derivatives, and integrals. The constant 'e' is pervasive in calculus.
- Physics: Many physical constants and formulas involve irrational numbers. For example, the golden ratio appears in the arrangement of leaves on a stem.
- Number Theory: The study of irrational numbers is a significant branch of number theory, exploring their properties and relationships with other numbers.
Conclusion: An Infinite Realm of Mystery
The interval between 1 and 6 contains an infinite number of irrational numbers, each with its unique and fascinating properties. While we've explored some prominent examples, the vast majority remain undiscovered and uncharacterized. The exploration of irrational numbers remains an ongoing journey, constantly revealing new depths and intricacies within the realm of mathematics. Their importance in mathematics, science, and even art highlights their significant role in our understanding of the world around us. The seemingly simple question "What are the irrational numbers between 1 and 6?" leads to a boundless exploration of mathematical concepts, showcasing the infinite beauty and complexity inherent in the number system.
Latest Posts
Latest Posts
-
How To Find Relative Maxima And Minima
Apr 03, 2025
-
How Do I Convert 3 8 Into A Decimal
Apr 03, 2025
-
What Is The Value Of H 2
Apr 03, 2025
-
What Is The Common Factor Of 8 And 12
Apr 03, 2025
-
2 5 As A Decimal And Percent
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Irrational Numbers Between 1 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
