How To Find Relative Maxima And Minima
listenit
Apr 03, 2025 · 5 min read
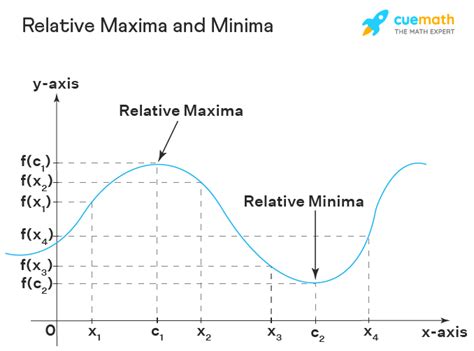
Table of Contents
How to Find Relative Maxima and Minima: A Comprehensive Guide
Finding relative maxima and minima is a crucial concept in calculus, with applications spanning diverse fields like optimization problems in engineering, economics, and machine learning. This comprehensive guide will walk you through the process, covering various methods and providing ample examples to solidify your understanding.
Understanding Relative Extrema
Before diving into the methods, let's define our terms. A relative maximum (or local maximum) is a point where the function's value is greater than or equal to the values at all nearby points. Similarly, a relative minimum (or local minimum) is a point where the function's value is less than or equal to the values at all nearby points. Collectively, these points are called relative extrema. It's crucial to distinguish relative extrema from absolute extrema, which are the highest and lowest points across the entire domain of the function.
Important Note: A relative extremum can exist at a point where the derivative is undefined, for instance, at a sharp corner or cusp in a function's graph.
Method 1: Using the First Derivative Test
This method relies on analyzing the sign changes of the first derivative, f'(x). The core idea is that:
- At a relative maximum: The function increases before the critical point and decreases afterward. This means the first derivative changes from positive to negative.
- At a relative minimum: The function decreases before the critical point and increases afterward. This means the first derivative changes from negative to positive.
Steps:
- Find the first derivative, f'(x).
- Find the critical points. These are points where f'(x) = 0 or f'(x) is undefined.
- Analyze the sign of f'(x) around each critical point. Create a sign chart to visualize the intervals where f'(x) is positive (increasing function) or negative (decreasing function).
- Identify relative extrema based on sign changes. If the sign changes from positive to negative, you have a relative maximum. If it changes from negative to positive, you have a relative minimum. If the sign doesn't change, it's neither.
Example:
Let's consider the function f(x) = x³ - 3x + 2.
-
Find f'(x): f'(x) = 3x² - 3
-
Find critical points: Set f'(x) = 0: 3x² - 3 = 0 => x² = 1 => x = ±1.
-
Analyze the sign of f'(x):
Interval (-∞, -1) (-1, 1) (1, ∞) f'(x) Positive Negative Positive f(x) Increasing Decreasing Increasing -
Identify extrema: At x = -1, f'(x) changes from positive to negative, indicating a relative maximum. At x = 1, f'(x) changes from negative to positive, indicating a relative minimum.
Method 2: Using the Second Derivative Test
This method uses the second derivative, f''(x), to determine the nature of critical points.
Steps:
- Find the first derivative, f'(x), and set it to zero to find critical points.
- Find the second derivative, f''(x).
- Evaluate f''(x) at each critical point.
- If f''(x) > 0, the critical point is a relative minimum.
- If f''(x) < 0, the critical point is a relative maximum.
- If f''(x) = 0, the test is inconclusive; you must use the first derivative test.
Example:
Let's use the same function as before: f(x) = x³ - 3x + 2.
- Critical points: We already know the critical points are x = ±1.
- Find f''(x): f''(x) = 6x
- Evaluate f''(x) at critical points:
- At x = -1, f''(-1) = -6 < 0, indicating a relative maximum.
- At x = 1, f''(1) = 6 > 0, indicating a relative minimum.
This confirms the results obtained using the first derivative test.
Method 3: Analyzing the Graph (Visual Inspection)
For simple functions, you can often identify relative maxima and minima by visually inspecting their graph. A relative maximum appears as a "peak," while a relative minimum appears as a "valley." This method is less precise and is primarily useful for quick visual checks or when dealing with graphically simple functions. However, it's important to remember that visual inspection might miss subtle extrema, especially with complex functions.
Handling Functions with Undefined Derivatives
Remember, critical points can occur where the derivative is undefined. These points often correspond to sharp corners, cusps, or vertical tangents. In such cases, the second derivative test is not applicable, and you must rely on the first derivative test or a careful analysis of the function's behavior around the point.
Extending to Functions of Multiple Variables
Finding relative extrema for functions of multiple variables (e.g., f(x, y)) requires more advanced techniques involving partial derivatives and the Hessian matrix. The process involves finding critical points by setting the gradient (vector of partial derivatives) to zero and then using the Hessian matrix (matrix of second partial derivatives) to classify these points as relative maxima, minima, or saddle points. This is beyond the scope of this introductory guide, but represents a natural extension of the concepts discussed.
Applications of Finding Relative Extrema
The ability to find relative maxima and minima has wide-ranging applications:
- Optimization Problems: In engineering, finding the minimum cost or maximum efficiency often involves finding the relative minimum or maximum of a function representing cost or efficiency.
- Economics: Maximizing profit or minimizing loss often translates to finding the relative maximum or minimum of a profit or cost function.
- Machine Learning: Many optimization algorithms in machine learning, such as gradient descent, rely on iteratively finding relative minima of a loss function.
- Physics: Determining equilibrium points in physical systems often involves finding the relative minima of a potential energy function.
Conclusion
Finding relative maxima and minima is a fundamental concept in calculus with significant practical implications. Mastering the first and second derivative tests provides you with powerful tools to solve a wide range of optimization problems. Remember to carefully analyze the function's behavior around critical points, especially those where the derivative is undefined. While graphical inspection can be helpful for simpler functions, relying on the derivative tests ensures accuracy and allows you to handle more complex scenarios. Understanding these techniques equips you to tackle optimization problems across diverse fields and deepen your understanding of calculus's practical applications.
Latest Posts
Latest Posts
-
What Unit Is Used To Measure Force
Apr 04, 2025
-
Molar Mass Of Ba No3 2
Apr 04, 2025
-
Difference Between Chemical And Nuclear Reaction
Apr 04, 2025
-
3 And 1 8 As A Decimal
Apr 04, 2025
-
What Is The Greatest Common Factor Of 42 And 24
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about How To Find Relative Maxima And Minima . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
