What Is The Common Factor Of 8 And 12
listenit
Apr 03, 2025 · 5 min read
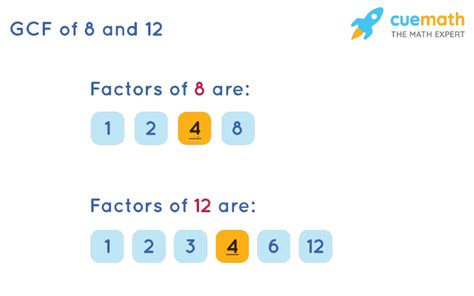
Table of Contents
What is the Common Factor of 8 and 12? A Deep Dive into Number Theory
Finding the common factor of 8 and 12 might seem like a simple task, suitable only for elementary school math. However, understanding this seemingly basic concept opens the door to a fascinating world of number theory, with implications far beyond simple arithmetic. This article will not only answer the question directly but also explore the broader mathematical concepts involved, including factors, divisors, greatest common divisors (GCD), and their applications in various fields.
Understanding Factors and Divisors
Before we delve into the specifics of 8 and 12, let's establish a solid foundation. In mathematics, a factor (or divisor) of a number is a whole number that divides that number without leaving a remainder. For example:
- Factors of 8: 1, 2, 4, and 8. These numbers divide 8 evenly.
- Factors of 12: 1, 2, 3, 4, 6, and 12. These numbers divide 12 evenly.
Notice that some numbers appear in both lists. These are the common factors of 8 and 12.
Identifying Common Factors of 8 and 12
By comparing the lists of factors for 8 and 12, we can easily identify their common factors:
- 1: Divides both 8 and 12 evenly.
- 2: Divides both 8 and 12 evenly.
- 4: Divides both 8 and 12 evenly.
Therefore, the common factors of 8 and 12 are 1, 2, and 4.
Visualizing Factors with Prime Factorization
A powerful tool for understanding factors is prime factorization. Prime factorization is the process of expressing a number as the product of its prime factors (prime numbers are whole numbers greater than 1 that are only divisible by 1 and themselves).
- Prime factorization of 8: 2 x 2 x 2 = 2³
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
By comparing the prime factorizations, we can see that both 8 and 12 share two factors of 2. This immediately tells us that 2² (which is 4) is a common factor. Since 1 is always a factor of any number, we can confidently say that 1, 2, and 4 are the common factors.
The Greatest Common Divisor (GCD)
Among the common factors, there's one that holds particular significance: the greatest common divisor (GCD). The GCD is the largest number that divides both numbers without leaving a remainder. In the case of 8 and 12, the GCD is 4.
Methods for Finding the GCD
Several methods can be used to determine the GCD:
- Listing Factors: This is the method we used above, suitable for smaller numbers.
- Prime Factorization: Comparing the prime factorizations allows us to identify the common prime factors and their lowest powers, which when multiplied, give the GCD.
- Euclidean Algorithm: This is an efficient algorithm for finding the GCD of larger numbers, especially when listing factors becomes cumbersome. The algorithm involves repeatedly applying the division algorithm until the remainder is zero. The last non-zero remainder is the GCD.
Let's illustrate the Euclidean Algorithm for 8 and 12:
- Divide the larger number (12) by the smaller number (8): 12 = 8 x 1 + 4
- Replace the larger number with the smaller number (8) and the smaller number with the remainder (4): 8 = 4 x 2 + 0
- Since the remainder is 0, the GCD is the last non-zero remainder, which is 4.
Applications of GCDs and Common Factors
The concept of GCDs and common factors extends far beyond simple arithmetic. They have practical applications in various fields:
1. Fraction Simplification
Finding the GCD allows us to simplify fractions to their lowest terms. For instance, the fraction 8/12 can be simplified by dividing both the numerator and denominator by their GCD (4), resulting in the equivalent fraction 2/3.
2. Cryptography
GCD plays a crucial role in certain cryptographic algorithms, such as the RSA algorithm, which is widely used for secure data transmission. The security of RSA depends on the difficulty of finding the GCD of two very large numbers.
3. Geometry and Measurement
Common factors are important in solving geometric problems. For example, when determining the dimensions of tiles needed to cover a rectangular area, the GCD helps find the largest possible tile size that fits evenly without any gaps.
4. Music Theory
The concept of common factors is applicable in music theory, where intervals are represented by ratios. Finding the GCD of the numerator and denominator of a ratio helps to simplify the representation of intervals and understand their relationships.
Beyond the Basics: Exploring Least Common Multiples (LCM)
While we've focused on common factors and GCDs, it's important to mention the least common multiple (LCM). The LCM is the smallest number that is a multiple of both numbers. For 8 and 12, the LCM is 24.
Understanding the relationship between GCD and LCM is crucial. There's a fascinating formula connecting them:
(Number 1) x (Number 2) = GCD x LCM
In our case: 8 x 12 = 4 x 24 = 96
This formula demonstrates the interconnectedness of these seemingly distinct concepts within number theory.
Conclusion: The Significance of Simple Concepts
The seemingly simple question of finding the common factors of 8 and 12 leads us on a journey through fundamental mathematical concepts with far-reaching applications. Understanding factors, divisors, GCDs, and LCMs is not merely an exercise in arithmetic; it's a cornerstone of number theory and a foundation for more advanced mathematical explorations in various fields. Mastering these concepts opens doors to a deeper appreciation of the elegant structure and surprising connections within the world of numbers. The seemingly trivial problem highlights the beauty and power of mathematical principles that underpin much of our technological and scientific advancements. From simple fraction simplification to complex cryptographic systems, the common factors of 8 and 12, and their GCD of 4, represent a fundamental concept with widespread significance.
Latest Posts
Latest Posts
-
What Unit Is Used To Measure Force
Apr 04, 2025
-
Molar Mass Of Ba No3 2
Apr 04, 2025
-
Difference Between Chemical And Nuclear Reaction
Apr 04, 2025
-
3 And 1 8 As A Decimal
Apr 04, 2025
-
What Is The Greatest Common Factor Of 42 And 24
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is The Common Factor Of 8 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
