2 5 As A Decimal And Percent
listenit
Apr 03, 2025 · 4 min read
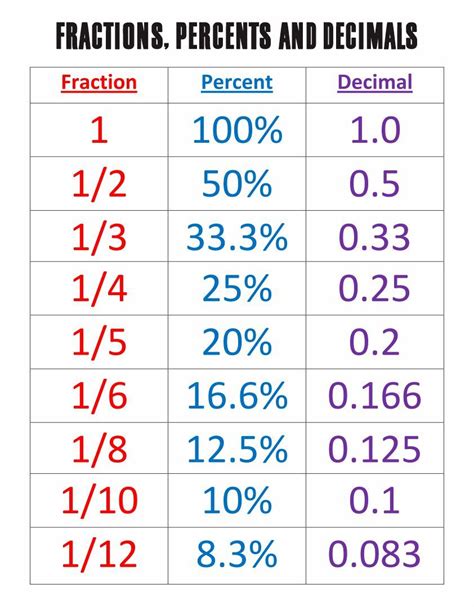
Table of Contents
2/5 as a Decimal and Percent: A Comprehensive Guide
Understanding fractions, decimals, and percentages is fundamental to various aspects of life, from everyday calculations to advanced mathematical concepts. This comprehensive guide will delve into the conversion of the fraction 2/5 into its decimal and percentage equivalents, exploring the underlying principles and providing practical applications. We'll also cover related concepts and techniques to solidify your understanding.
Understanding Fractions, Decimals, and Percentages
Before diving into the conversion of 2/5, let's briefly review the definitions of these three crucial mathematical representations:
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of equal parts, while the numerator shows the number of parts considered. For example, in the fraction 2/5, 2 is the numerator and 5 is the denominator.
Decimals: Decimals are another way to represent parts of a whole. They use a base-ten system, with the digits to the right of the decimal point representing tenths, hundredths, thousandths, and so on. For instance, 0.5 represents five-tenths, and 0.25 represents twenty-five hundredths.
Percentages: Percentages represent a fraction or decimal as a portion of 100. The symbol "%" is used to denote percentage. For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Converting 2/5 to a Decimal
Converting a fraction to a decimal involves dividing the numerator by the denominator. In the case of 2/5:
- Divide the numerator (2) by the denominator (5): 2 ÷ 5 = 0.4
Therefore, 2/5 as a decimal is 0.4.
Converting 2/5 to a Percentage
There are two primary methods for converting a fraction to a percentage:
Method 1: Using the Decimal Equivalent
- Convert the fraction to a decimal (as shown above): 2/5 = 0.4
- Multiply the decimal by 100: 0.4 x 100 = 40
- Add the percentage symbol: 40%
Therefore, 2/5 as a percentage is 40%.
Method 2: Direct Conversion
This method involves finding an equivalent fraction with a denominator of 100.
- Find the factor to multiply the denominator by to get 100: 5 x 20 = 100
- Multiply both the numerator and denominator by this factor: (2 x 20) / (5 x 20) = 40/100
- The numerator of the equivalent fraction represents the percentage: 40%
Therefore, 2/5 as a percentage is 40%. Both methods yield the same result.
Practical Applications of 2/5, 0.4, and 40%
Understanding the equivalence between 2/5, 0.4, and 40% allows for flexible problem-solving in various contexts:
- Calculating discounts: A 40% discount on a $100 item means a reduction of $40 (40% of $100).
- Determining proportions: If 2 out of 5 students in a class prefer a particular subject, this represents 40% of the class.
- Analyzing data: Representing data as percentages facilitates comparisons and interpretations. For example, if 40% of respondents to a survey chose a certain option, it provides a clear picture of their preferences.
- Financial calculations: Interest rates, loan repayments, and investment returns are often expressed as percentages. Understanding the fractional and decimal equivalents aids in precise calculations.
- Measurement and scaling: Scaling down blueprints or maps often involves converting fractions to decimals or percentages.
Further Exploration: Converting Other Fractions
The principles discussed above can be applied to convert other fractions to decimals and percentages. Let's consider some examples:
1/4:
- Decimal: 1 ÷ 4 = 0.25
- Percentage: 0.25 x 100 = 25%
3/8:
- Decimal: 3 ÷ 8 = 0.375
- Percentage: 0.375 x 100 = 37.5%
7/10:
- Decimal: 7 ÷ 10 = 0.7
- Percentage: 0.7 x 100 = 70%
Dealing with Recurring Decimals
Some fractions, when converted to decimals, result in recurring decimals (decimals with repeating patterns). For example, 1/3 = 0.333... In such cases, it's often sufficient to round the decimal to a certain number of decimal places for practical applications.
Advanced Concepts: Percentage Change and Percentage Points
Beyond basic conversions, understanding percentage change and percentage points is crucial in many analytical situations.
Percentage Change: This measures the relative change between two values. The formula is:
[(New Value - Old Value) / Old Value] x 100
For example, if a value increases from 50 to 60, the percentage change is:
[(60 - 50) / 50] x 100 = 20%
Percentage Points: This refers to the absolute difference between two percentages. For example, if the unemployment rate increases from 5% to 8%, it has increased by 3 percentage points, not 60% (which would be the percentage change).
Conclusion: Mastering Fractions, Decimals, and Percentages
The ability to seamlessly convert between fractions, decimals, and percentages is an essential skill in various fields. Understanding the underlying principles and practicing different conversion methods will improve your mathematical proficiency and problem-solving abilities. This guide has provided a comprehensive overview, including practical examples and advanced concepts, to help you master these fundamental mathematical tools. Remember to practice regularly and apply your knowledge in real-world scenarios to solidify your understanding.
Latest Posts
Latest Posts
-
Is A Change In Color A Chemical Change
Apr 04, 2025
-
What Happens To An Animal Cell In A Isotonic Solution
Apr 04, 2025
-
Find A Cartesian Equation For The Curve
Apr 04, 2025
-
Abiotic Factor How To Get Water
Apr 04, 2025
-
Three Parts Of An Atp Molecule
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about 2 5 As A Decimal And Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
