What Is The Improper Fraction Of 2 1/4
listenit
Apr 01, 2025 · 6 min read
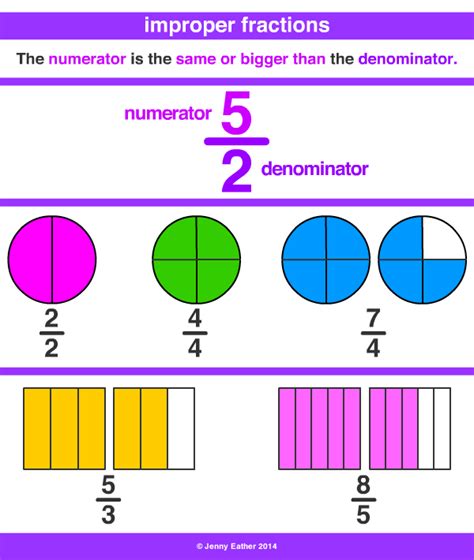
Table of Contents
What is the Improper Fraction of 2 1/4? A Deep Dive into Fraction Conversion
Understanding fractions is fundamental to mathematics, and converting between mixed numbers and improper fractions is a crucial skill. This comprehensive guide will not only answer the question, "What is the improper fraction of 2 1/4?" but will also equip you with the knowledge and strategies to tackle similar conversions confidently. We'll explore the concepts in detail, providing multiple examples and addressing common misconceptions.
Understanding Mixed Numbers and Improper Fractions
Before diving into the conversion, let's define our terms.
Mixed Number: A mixed number combines a whole number and a proper fraction. For example, 2 1/4 is a mixed number; it represents two whole units and one-quarter of another unit.
Improper Fraction: An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). For example, 9/4 is an improper fraction. It represents more than one whole unit.
The key difference lies in the representation. A mixed number is a convenient way to visualize quantities, while an improper fraction is often more useful for mathematical operations like addition, subtraction, multiplication, and division.
Converting 2 1/4 to an Improper Fraction: The Step-by-Step Process
The conversion of 2 1/4 to an improper fraction involves two simple steps:
Step 1: Multiply the whole number by the denominator.
In our example, the whole number is 2, and the denominator of the fraction is 4. Multiplying these gives us 2 * 4 = 8.
Step 2: Add the numerator to the result from Step 1.
The numerator of our fraction is 1. Adding this to the result from Step 1 gives us 8 + 1 = 9.
Step 3: Keep the denominator the same.
The denominator remains unchanged throughout the conversion process. Therefore, the denominator stays as 4.
Step 4: Combine the results to form the improper fraction.
Combining the results from Step 2 and Step 3 gives us the improper fraction 9/4.
Therefore, the improper fraction of 2 1/4 is 9/4.
Visualizing the Conversion
It's helpful to visualize the conversion. Imagine you have two whole pizzas and one-quarter of another pizza. If you were to cut each pizza into four equal slices, you would have a total of (2 * 4) + 1 = 9 slices. Since each slice represents one-quarter of a pizza, you have 9/4 pizzas.
Practical Applications and Real-World Examples
Understanding the conversion between mixed numbers and improper fractions is essential in various real-world scenarios. Here are a few examples:
-
Baking: Recipes often call for fractional amounts of ingredients. Converting mixed numbers to improper fractions simplifies calculations when scaling up or down a recipe. For instance, if a recipe calls for 2 1/4 cups of flour and you need to double the recipe, converting 2 1/4 to 9/4 makes the calculation easier (9/4 * 2 = 18/4 = 4 2/4 = 4 1/2 cups).
-
Construction and Measurement: Construction projects often involve precise measurements. Converting between mixed numbers and improper fractions ensures accurate calculations when dealing with lengths, areas, or volumes. Imagine calculating the area of a rectangular plot of land measuring 2 1/4 meters by 3 meters. Converting 2 1/4 to 9/4 simplifies the area calculation (9/4 * 3 = 27/4 = 6 3/4 square meters).
-
Sewing and Fabric Cutting: Tailors and seamstresses frequently work with fractional measurements. Converting mixed numbers to improper fractions allows for more accurate calculations when cutting fabric and ensuring proper garment fit.
-
Financial Calculations: Many financial calculations, particularly those involving interest rates and shares, involve fractions. Converting between mixed numbers and improper fractions ensures accuracy and simplifies the calculations.
Beyond 2 1/4: Mastering the Conversion Process
The method described above can be applied to any mixed number. Let's practice with a few more examples:
Example 1: Converting 3 2/5 to an improper fraction
- Multiply the whole number by the denominator: 3 * 5 = 15
- Add the numerator: 15 + 2 = 17
- Keep the denominator: 5
- The improper fraction is 17/5
Example 2: Converting 1 7/8 to an improper fraction
- Multiply the whole number by the denominator: 1 * 8 = 8
- Add the numerator: 8 + 7 = 15
- Keep the denominator: 8
- The improper fraction is 15/8
Example 3: Converting 5 1/3 to an improper fraction
- Multiply the whole number by the denominator: 5 * 3 = 15
- Add the numerator: 15 + 1 = 16
- Keep the denominator: 3
- The improper fraction is 16/3
Common Mistakes and How to Avoid Them
While the conversion process is straightforward, some common mistakes can occur:
-
Forgetting to add the numerator: Remember that the numerator represents a part of a whole and must be added to the product of the whole number and the denominator.
-
Changing the denominator: The denominator remains unchanged throughout the conversion.
-
Incorrect multiplication: Double-check your multiplication of the whole number and the denominator to ensure accuracy.
-
Improper simplification: Always simplify the resulting improper fraction to its lowest terms if possible. For example, 18/6 should be simplified to 3.
Converting Improper Fractions back to Mixed Numbers
The reverse process, converting an improper fraction back to a mixed number, is equally important. To do this:
-
Divide the numerator by the denominator. The quotient represents the whole number part of the mixed number.
-
The remainder becomes the numerator of the fraction.
-
The denominator remains the same.
For example, let's convert 9/4 back to a mixed number:
-
Divide 9 by 4: 9 ÷ 4 = 2 with a remainder of 1.
-
The whole number is 2.
-
The remainder (1) is the new numerator.
-
The denominator remains 4.
Therefore, 9/4 = 2 1/4.
Conclusion: Mastering Fractions for Mathematical Success
Understanding the conversion between mixed numbers and improper fractions is crucial for success in mathematics and various real-world applications. By mastering this fundamental skill, you'll be better equipped to handle more complex mathematical problems and confidently tackle challenges involving fractions. Remember the simple steps, practice regularly, and visualize the process to solidify your understanding. With consistent practice, you'll confidently navigate the world of fractions and unlock their potential in your everyday life. This thorough understanding of improper fractions and their relationship with mixed numbers will serve you well in your academic and professional pursuits. Remember to practice regularly and you'll become proficient in converting between these two important fractional forms.
Latest Posts
Latest Posts
-
Which Two Subatomic Particles Are Located In The Nucleus
Apr 02, 2025
-
Irrational Numbers Between 1 And 6
Apr 02, 2025
-
In A Hypertonic Solution A Cell Will
Apr 02, 2025
-
How Many Kilograms Are In 5000 Grams
Apr 02, 2025
-
Solve This Inequality 3b 7 32
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is The Improper Fraction Of 2 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
