What Is The Area Of This Circle In Square Centimeters
listenit
Apr 01, 2025 · 5 min read
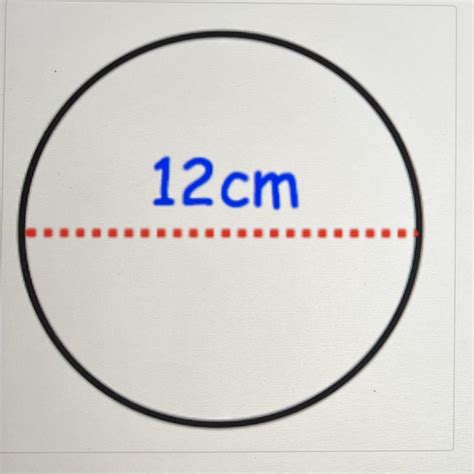
Table of Contents
What is the Area of This Circle in Square Centimeters? A Comprehensive Guide
Determining the area of a circle is a fundamental concept in geometry with wide-ranging applications in various fields. This comprehensive guide will delve into the intricacies of calculating the area of a circle, providing you with not only the formula but also a deep understanding of its derivation, practical applications, and troubleshooting common misconceptions. We'll explore different scenarios, including how to handle situations where you're given the diameter or circumference instead of the radius. Finally, we'll tackle some example problems to solidify your understanding and equip you with the skills to solve similar problems with confidence.
Understanding the Basics: Radius, Diameter, and Circumference
Before diving into the area calculation, let's establish a clear understanding of the fundamental components of a circle:
-
Radius (r): The distance from the center of the circle to any point on the circle. It's a crucial element in the area calculation.
-
Diameter (d): The distance across the circle passing through the center. The diameter is always twice the radius (d = 2r).
-
Circumference (C): The distance around the circle. It's calculated using the formula C = 2πr, where π (pi) is approximately 3.14159.
The Formula for the Area of a Circle
The area (A) of a circle is calculated using the following formula:
A = πr²
This formula means that the area of a circle is equal to pi multiplied by the square of its radius. Understanding this formula is the cornerstone of successfully calculating the area of any circle.
Derivation of the Formula: A Visual Explanation
While the formula itself is relatively straightforward, understanding its derivation provides a deeper appreciation of its meaning. Imagine dividing the circle into numerous thin concentric rings. Each ring can be approximated as a rectangle with a length equal to the circumference of that ring and a width equal to the small radial distance (dr). The area of each ring is then approximately (2πr)(dr). Summing the areas of all these rings as the width (dr) approaches zero gives us the integral:
∫₀ᴿ 2πrdr = πr²
This integral elegantly demonstrates that the area of a circle is indeed πr².
Calculating the Area: Step-by-Step Guide
Let's break down the process of calculating the area of a circle into simple, manageable steps:
-
Identify the Radius: The first and most crucial step is to determine the radius (r) of the circle. This value might be given directly, or you might need to calculate it from the diameter (r = d/2) or circumference (r = C/2π).
-
Square the Radius: Square the value of the radius (r²).
-
Multiply by Pi: Multiply the squared radius by π (approximately 3.14159). You can use a calculator for greater accuracy.
-
State the Units: Remember to include the appropriate units in your final answer (e.g., square centimeters, square meters, square inches). The area is always expressed in square units.
Example Problem 1: Radius Provided
Let's say we have a circle with a radius of 5 centimeters. What is its area?
-
Radius (r): 5 cm
-
Square the Radius (r²): 5² = 25 cm²
-
Multiply by Pi: 25 cm² * π ≈ 78.54 cm²
Therefore, the area of the circle is approximately 78.54 square centimeters.
Example Problem 2: Diameter Provided
A circle has a diameter of 12 meters. What is its area?
-
Diameter (d): 12 m
-
Calculate the Radius (r): r = d/2 = 12 m / 2 = 6 m
-
Square the Radius (r²): 6² = 36 m²
-
Multiply by Pi: 36 m² * π ≈ 113.10 m²
Therefore, the area of the circle is approximately 113.10 square meters.
Example Problem 3: Circumference Provided
The circumference of a circle is 25 inches. Find its area.
-
Circumference (C): 25 inches
-
Calculate the Radius (r): r = C / 2π ≈ 25 inches / (2 * 3.14159) ≈ 3.98 inches
-
Square the Radius (r²): 3.98² ≈ 15.84 inches²
-
Multiply by Pi: 15.84 inches² * π ≈ 49.74 inches²
Therefore, the area of the circle is approximately 49.74 square inches.
Dealing with Real-World Applications
The ability to calculate the area of a circle is crucial in many real-world applications, including:
-
Engineering: Calculating the cross-sectional area of pipes, cylinders, and other circular components.
-
Construction: Determining the amount of material needed for circular structures such as domes or foundations.
-
Agriculture: Estimating the area of irrigated land or the space needed for circular crops.
-
Design: In graphic design and other visual arts, it’s fundamental for calculating the size and proportions of circular elements.
Troubleshooting Common Mistakes
-
Forgetting to Square the Radius: This is a very common mistake. Remember that the formula is πr², not πr.
-
Incorrect Unit Conversion: Ensure that all measurements are in the same units before calculating the area. If given a diameter in feet and asked for the area in square inches, convert the diameter to inches before calculating the radius and area.
-
Using an Inaccurate Value of Pi: While 3.14 is a common approximation, using a more precise value (like 3.14159 or the π button on your calculator) will result in a more accurate answer, especially when dealing with larger circles.
Advanced Concepts: Sectors and Segments
The formula for the area of a circle can also be used to calculate the area of sectors and segments of a circle.
-
Sector: A sector is a portion of a circle enclosed by two radii and an arc. Its area is a fraction of the circle's area, proportional to the central angle. The formula is: Area of sector = (θ/360°) * πr², where θ is the central angle in degrees.
-
Segment: A segment is the area between a chord and an arc. To find its area, you first find the area of the sector formed by the same arc and radii, then subtract the area of the triangle formed by the chord and the radii.
Conclusion: Mastering Circle Area Calculations
Understanding how to calculate the area of a circle is a valuable skill with numerous practical applications. By mastering the formula, understanding its derivation, and practicing with different examples, you'll confidently tackle any circle area problem. Remember to pay attention to units, carefully follow the steps, and utilize a calculator for greater precision when necessary. This detailed guide has equipped you with the knowledge and tools to not only solve area problems but also understand the underlying mathematical principles. Keep practicing, and you'll become proficient in this essential geometric concept.
Latest Posts
Latest Posts
-
How To Find N In Pv Nrt
Apr 02, 2025
-
Why Does Ionization Decrease Down A Group
Apr 02, 2025
-
What Is The Square Root Of 576
Apr 02, 2025
-
How To Find X Intercepts Of A Quadratic Equation
Apr 02, 2025
-
Which Electromagnetic Radiation Has The Shortest Wavelength
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is The Area Of This Circle In Square Centimeters . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
