6 1/2 As An Improper Fraction
listenit
Mar 31, 2025 · 5 min read
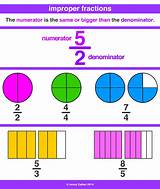
Table of Contents
6 1/2 as an Improper Fraction: A Comprehensive Guide
Understanding how to convert mixed numbers, like 6 1/2, into improper fractions is a fundamental skill in mathematics. This seemingly simple conversion forms the basis for many more complex calculations and is crucial for various applications, from baking to engineering. This article delves deep into the process, providing multiple methods, real-world examples, and addressing common misconceptions to ensure a complete understanding of this crucial mathematical concept.
What is a Mixed Number?
A mixed number combines a whole number and a fraction. It represents a quantity greater than one. For instance, 6 1/2 signifies six whole units plus an additional half unit. The whole number (6 in this case) represents complete units, while the fraction (1/2) represents a part of a unit.
What is an Improper Fraction?
An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). Unlike mixed numbers, improper fractions represent a quantity greater than or equal to one. For example, 13/2 is an improper fraction because the numerator (13) is larger than the denominator (2).
Converting 6 1/2 to an Improper Fraction: The Step-by-Step Method
Converting a mixed number to an improper fraction involves a straightforward two-step process:
Step 1: Multiply the whole number by the denominator.
In our example, 6 1/2, we multiply the whole number (6) by the denominator of the fraction (2): 6 * 2 = 12
Step 2: Add the numerator to the result from Step 1.
Next, we add the numerator of the fraction (1) to the result from Step 1: 12 + 1 = 13
Step 3: Write the result as the numerator over the original denominator.
Finally, we write the result (13) as the numerator and keep the original denominator (2) unchanged. This gives us our improper fraction: 13/2
Therefore, 6 1/2 as an improper fraction is 13/2.
Visualizing the Conversion
Imagine you have six and a half pizzas. Each pizza is divided into two equal slices. You have six whole pizzas, each with two slices, totaling 6 * 2 = 12 slices. Plus, you have an additional half pizza, which is one slice. In total, you have 12 + 1 = 13 slices. Since each pizza has two slices, you have 13/2 pizzas, representing the improper fraction.
Alternative Methods for Conversion
While the above method is the most common and straightforward, here are a couple of alternative approaches to understand the concept better:
Method 1: Using the concept of equivalent fractions:
We can represent 6 as a fraction with a denominator of 2: 6 = 12/2 (since 12 divided by 2 equals 6). Then, we add the fraction 1/2: 12/2 + 1/2 = 13/2
This method emphasizes the idea of finding an equivalent fraction for the whole number before combining it with the fractional part.
Method 2: Understanding the relationship between mixed numbers and improper fractions:
A mixed number is simply a shorthand representation of an addition problem involving a whole number and a fraction. The improper fraction is the simplified result of that addition expressed as a single fraction.
Real-World Applications of Improper Fractions
Improper fractions are not merely abstract mathematical concepts; they have practical applications in various fields:
-
Baking and Cooking: Recipes often call for fractional amounts of ingredients. Converting mixed numbers to improper fractions simplifies calculations when scaling recipes up or down. For example, if a recipe requires 2 1/2 cups of flour and you want to double it, converting 2 1/2 to 5/2 makes the calculation much easier (5/2 * 2 = 5 cups).
-
Construction and Engineering: Precise measurements are paramount in construction and engineering. Working with improper fractions streamlines calculations involving lengths, areas, and volumes, ensuring accuracy in blueprints and designs.
-
Finance and Accounting: Dealing with portions of money, shares, or other financial units frequently necessitates the use of fractions, including improper fractions, for accurate calculations of interest, profits, or losses.
-
Data Analysis and Statistics: In various statistical calculations and data representations, improper fractions often simplify the representation and manipulation of data sets.
-
Computer Science and Programming: Many programming algorithms and data structures involve fractional calculations, where improper fractions provide efficient representation and processing of numerical values.
Common Mistakes and How to Avoid Them
Several common mistakes can occur when converting mixed numbers to improper fractions:
-
Forgetting to add the numerator: A common error is to multiply the whole number by the denominator but forget to add the numerator. Always remember the crucial addition step.
-
Incorrectly placing the numerator and denominator: Ensure the result of the addition (from Step 2) becomes the new numerator and the original denominator remains unchanged.
-
Not simplifying the resulting improper fraction: Sometimes the resulting improper fraction can be simplified further. Remember to reduce the fraction to its lowest terms if possible. For example, 14/4 can be simplified to 7/2.
Advanced Applications and Extensions
Understanding improper fractions opens the door to more complex mathematical operations:
-
Adding and Subtracting Mixed Numbers: Converting mixed numbers to improper fractions simplifies these operations. This is because adding or subtracting fractions requires a common denominator, and the conversion makes it easier to find one.
-
Multiplying and Dividing Mixed Numbers: Similar to addition and subtraction, converting to improper fractions significantly simplifies these operations.
-
Working with Algebraic Expressions: The concepts extend to algebraic expressions where variables may be involved in the mixed numbers.
-
Solving Equations: Many equation solving problems involve fractions, and converting to improper fractions can simplify the solutions.
Conclusion: Mastering the Conversion of 6 1/2
Mastering the conversion of mixed numbers like 6 1/2 to improper fractions (13/2) is crucial for progressing in mathematics and applying these concepts in various real-world contexts. By understanding the step-by-step process, visualizing the concept, and avoiding common mistakes, you'll build a solid foundation for more advanced mathematical tasks and problem-solving. Remember the practical significance of this skill across numerous disciplines – from baking a perfect cake to designing a sturdy bridge, the ability to confidently handle fractions is invaluable. Practice regularly and soon you'll be converting mixed numbers to improper fractions with ease and accuracy.
Latest Posts
Latest Posts
-
How Many Cc In 10 Ml
Apr 01, 2025
-
Number Of Valence Electrons For Silicon
Apr 01, 2025
-
What Is The Area Of This Circle In Square Centimeters
Apr 01, 2025
-
What Is The Improper Fraction Of 2 1 4
Apr 01, 2025
-
Lewis Acid Vs Bronsted Lowry Acid
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about 6 1/2 As An Improper Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
