2 Times Square Root Of 5
listenit
Apr 01, 2025 · 5 min read
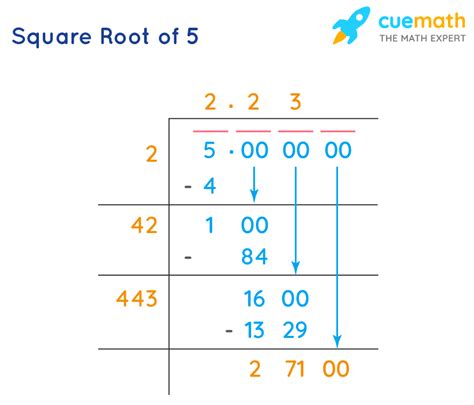
Table of Contents
Decoding 2√5: A Deep Dive into the Number and its Applications
The seemingly simple expression "2√5" hides a wealth of mathematical richness and practical applications. This seemingly innocuous number, approximately equal to 4.472, appears frequently in various fields, from geometry and physics to computer graphics and engineering. This article will delve deep into the nature of 2√5, exploring its properties, calculations, and its surprising prevalence across diverse disciplines.
Understanding the Basics: Square Roots and Irrational Numbers
Before embarking on a detailed exploration of 2√5, let's solidify our understanding of its fundamental components: square roots and irrational numbers.
What is a Square Root?
The square root of a number 'x' is a value that, when multiplied by itself, equals 'x'. For example, the square root of 9 (√9) is 3, because 3 * 3 = 9. Square roots can be represented by the radical symbol (√) or as a fractional exponent (e.g., x<sup>1/2</sup>).
Irrational Numbers: The Nature of √5
Not all numbers have neat, whole-number square roots. The square root of 5 (√5) is an irrational number. This means it cannot be expressed as a simple fraction (a ratio of two integers). Its decimal representation continues infinitely without repeating: approximately 2.236067977... This infinite, non-repeating nature is a defining characteristic of irrational numbers.
2√5: A Scaled Irrational Number
2√5 simply represents two times the square root of 5. We can think of it as scaling the irrational number √5 by a factor of 2. This scaling doesn't alter the fundamental nature of the number; it remains irrational. Its approximate value is 2 * 2.236... ≈ 4.472.
Calculating 2√5: Methods and Approximations
While the exact value of 2√5 is irrational and cannot be fully represented, we can calculate approximations using several methods.
Using a Calculator: The Easiest Method
The simplest method is to use a calculator. Most calculators have a square root function (√) allowing for a direct calculation: enter 5, press the square root button, then multiply the result by 2. This gives a readily usable approximation, usually to several decimal places.
Manual Approximation: Babylonian Method
For a deeper understanding, we can explore approximation methods like the Babylonian method (also known as Heron's method). This iterative approach refines an initial guess to progressively closer approximations of the square root.
Steps:
- Make an initial guess: Let's guess that √5 is approximately 2.
- Improve the guess: Divide 5 by the initial guess (5/2 = 2.5).
- Average the guess and the result: Average the initial guess and the result from step 2: (2 + 2.5) / 2 = 2.25.
- Repeat steps 2 and 3: Use 2.25 as the new guess and repeat the process. Each iteration will yield a closer approximation.
This method demonstrates the underlying process of approximating square roots, though calculators provide a far quicker and more precise result.
Geometrical Interpretations of 2√5
2√5 finds intriguing applications in geometry. Its appearance is often connected to specific geometric figures and calculations.
The Golden Ratio and Related Constructions
The golden ratio (approximately 1.618) is a famous mathematical constant appearing in nature and art. While not directly involving 2√5, constructions related to the golden ratio often indirectly utilize numbers like it in the calculations of lengths and proportions.
Right-Angled Triangles and Pythagorean Theorem
The Pythagorean theorem (a² + b² = c²) is crucial in right-angled triangles. Certain right-angled triangles have side lengths related to 2√5. For instance, a triangle with sides a and b such that a² + b² = 20 would have a hypotenuse (c) of length 2√5.
Other Geometric Applications
Beyond specific triangles, 2√5 could appear in various geometrical calculations involving distances, areas, and volumes, especially within more complex shapes and three-dimensional constructions. Its presence often arises from the interplay of squares and square roots within geometric formulas.
Applications of 2√5 in Various Fields
The seemingly abstract number 2√5 surfaces in surprisingly diverse fields. Let's explore some of these applications:
Physics and Engineering
In physics and engineering, 2√5 might arise in calculations involving vectors, forces, and distances. For instance, in analyzing the trajectory of a projectile or the stress on a structural component, the value could emerge during the calculation of magnitudes or components.
Computer Graphics and Game Development
Computer graphics heavily relies on mathematical calculations, especially for 3D rendering and animation. The value 2√5 could appear in algorithms determining the distances between points, object transformations, and camera movements. Accurate calculations involving such numbers are crucial for realistic rendering and smooth animation.
Architecture and Design
Similar to computer graphics, architectural design uses geometrical principles. 2√5 could play a part in calculations related to building dimensions, structural integrity, and aesthetically pleasing proportions, especially within designs influenced by geometric principles.
Financial Modeling and Data Analysis
Even in fields like finance, numbers like 2√5 might appear, particularly when dealing with complex mathematical models used for forecasting, risk assessment, or statistical analysis. The underlying equations often involve many factors, some of which could result in calculations that contain square roots, potentially including 2√5.
Beyond the Number: The Importance of Mathematical Exploration
While this article focuses on 2√5, its significance extends beyond its specific applications. Exploring seemingly simple numbers unveils underlying mathematical principles, enhancing our understanding of fundamental concepts like square roots, irrational numbers, and their role in various fields. This exploration fosters critical thinking and problem-solving skills applicable far beyond mathematics itself.
The exploration of 2√5 underscores the beauty and interconnectedness of mathematics. A number seemingly insignificant at first glance can reveal a fascinating tapestry of mathematical concepts and practical applications across diverse domains. The deeper we explore mathematical structures, the more we appreciate their subtle elegance and power in shaping our world. Even a seemingly simple number like 2√5 holds the key to unlocking deeper mathematical insights and understanding our world through a quantitative lens.
Latest Posts
Latest Posts
-
Instantaneous Rate Of Change Vs Average Rate Of Change
Apr 02, 2025
-
How Many D Orbitals Can Be In An Energy Level
Apr 02, 2025
-
Log Base 2 X 2 Graph
Apr 02, 2025
-
X 3 2x 2 5x 6
Apr 02, 2025
-
Is Boiling Water A Chemical Reaction
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about 2 Times Square Root Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
