X 3 6x 2 4x 24
listenit
Mar 26, 2025 · 5 min read
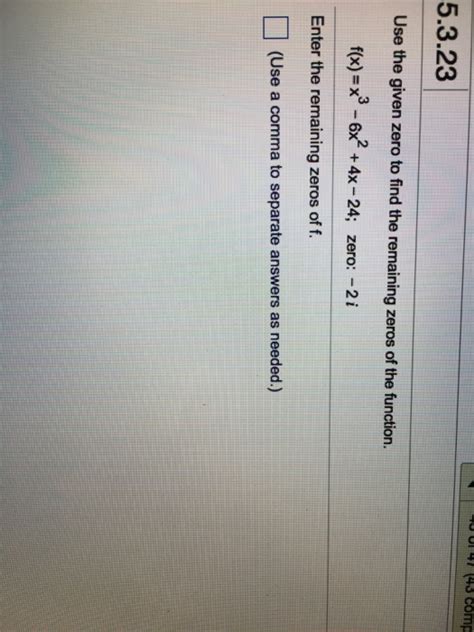
Table of Contents
Deconstructing the Expression: x³ + 6x² + 4x - 24
This article delves deep into the mathematical expression x³ + 6x² + 4x - 24, exploring its various facets, including factorization, root finding, graphing, and its applications in different fields. We'll dissect this seemingly simple cubic polynomial to reveal its hidden complexities and practical uses. Our approach will be comprehensive, incorporating both theoretical explanations and practical examples, making it accessible to a wide range of readers, from high school students to advanced mathematics enthusiasts.
Understanding Cubic Polynomials
Before diving into the specifics of x³ + 6x² + 4x - 24, let's establish a foundational understanding of cubic polynomials. A cubic polynomial is a polynomial of degree three, meaning the highest power of the variable (x in this case) is three. The general form is expressed as:
ax³ + bx² + cx + d = 0
where a, b, c, and d are constants, and 'a' is not equal to zero. Our specific expression, x³ + 6x² + 4x - 24, fits this general form with a=1, b=6, c=4, and d=-24.
Factorization Techniques
Finding the factors of a cubic polynomial is crucial for understanding its roots (the values of x that make the expression equal to zero). Several methods can be employed, including:
-
Rational Root Theorem: This theorem helps identify potential rational roots (roots that are fractions). It states that any rational root p/q (where p and q are integers and q ≠ 0) must satisfy the condition that p is a factor of the constant term (d) and q is a factor of the leading coefficient (a). In our case, the constant term is -24 and the leading coefficient is 1. Therefore, potential rational roots are the factors of -24: ±1, ±2, ±3, ±4, ±6, ±8, ±12, ±24.
-
Synthetic Division: Once a potential rational root is identified (using the Rational Root Theorem or through educated guesses), synthetic division is a quick and efficient method to check if it's a true root and to find the resulting quadratic factor.
-
Factoring by Grouping: This technique involves grouping terms to identify common factors and simplify the expression. While not always applicable, it's worth exploring.
Let's apply these methods to our expression, x³ + 6x² + 4x - 24.
Applying the Rational Root Theorem: We have several potential rational roots. Let's try x = 2:
- Substitute x = 2 into the expression: (2)³ + 6(2)² + 4(2) - 24 = 8 + 24 + 8 - 24 = 16. Not a root.
Let's try x = -2:
- Substitute x = -2: (-2)³ + 6(-2)² + 4(-2) - 24 = -8 + 24 - 8 - 24 = -16. Not a root.
Let's try x = -3:
- Substitute x = -3: (-3)³ + 6(-3)² + 4(-3) - 24 = -27 + 54 - 12 - 24 = -6. Not a root.
Let's try x = -4:
- Substitute x = -4: (-4)³ + 6(-4)² + 4(-4) - 24 = -64 + 96 - 16 - 24 = -8. Not a root.
Let's try x = 1:
- Substitute x = 1: (1)³ + 6(1)² + 4(1) - 24 = 1 + 6 + 4 - 24 = -13. Not a root.
Let's try x = -2:
- Substitute x = -2: (-2)³ + 6(-2)² + 4(-2) - 24 = -8 + 24 - 8 - 24 = -16
It appears that there are no easily identifiable rational roots. We might need to resort to more advanced techniques like numerical methods or the cubic formula to find the exact roots.
Numerical Methods for Root Finding:
Since simple factorization might not be straightforward, numerical methods such as the Newton-Raphson method or the bisection method can be employed to approximate the roots. These methods involve iterative calculations to progressively refine an initial guess until a root is found to a desired level of accuracy. These methods are generally implemented using computer software or calculators.
Graphing the Polynomial
Graphing the polynomial provides valuable visual insight into its behavior, including the approximate locations of its roots. By plotting the function y = x³ + 6x² + 4x - 24, we can observe its intercepts (where the graph crosses the x-axis), which represent the roots of the polynomial. The graph will reveal a cubic curve with potential turning points, indicating the presence of local maxima and minima. Online graphing calculators or mathematical software can be used for this purpose.
Applications of Cubic Polynomials
Cubic polynomials have numerous applications across various fields:
-
Engineering: Cubic equations are frequently encountered in engineering problems related to structural analysis, fluid dynamics, and electrical circuits. For example, determining the optimal dimensions of a structure or modeling the flow of fluids might involve solving cubic equations.
-
Physics: Cubic polynomials can be used to model various physical phenomena, such as the trajectory of a projectile or the motion of an object under the influence of certain forces.
-
Chemistry: In chemistry, cubic equations can be used in reaction kinetics and equilibrium calculations.
-
Economics: Cubic polynomials can be used to model complex economic relationships and optimize production or pricing strategies.
-
Computer Graphics: Cubic curves, based on cubic polynomials, are fundamental to computer graphics, used for creating smooth curves and surfaces in 3D modeling and animation.
Conclusion
The expression x³ + 6x² + 4x - 24, while seemingly simple at first glance, exemplifies the complexities and richness of cubic polynomials. Its factorization, root finding, and graphing require a blend of algebraic manipulation, numerical methods, and visual interpretation. Understanding such polynomials is crucial for tackling various problems across numerous disciplines, highlighting their significance in both theoretical mathematics and practical applications. While we haven't found the exact roots through elementary factorization methods here, the process of exploring various techniques and understanding their applications underscores the importance of a multifaceted approach to problem-solving in mathematics. Further exploration using numerical methods or specialized software would reveal the precise solutions.
Latest Posts
Latest Posts
-
What Does The Prefix Hydro Mean
Mar 29, 2025
-
How Do You Find The Equation Of A Secant Line
Mar 29, 2025
-
How Do You Factor 3x 2 5x 2
Mar 29, 2025
-
Whats The Atomic Number For Helium
Mar 29, 2025
-
Is Oxygen More Electronegative Than Carbon
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about X 3 6x 2 4x 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
