How Do You Find The Equation Of A Secant Line
listenit
Mar 29, 2025 · 6 min read
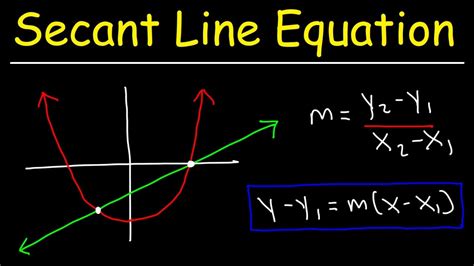
Table of Contents
How Do You Find the Equation of a Secant Line? A Comprehensive Guide
Finding the equation of a secant line is a fundamental concept in calculus and pre-calculus mathematics. Understanding this concept is crucial for grasping more advanced topics like derivatives and instantaneous rates of change. This comprehensive guide will walk you through the process step-by-step, providing clear explanations, examples, and helpful tips to master this skill.
What is a Secant Line?
A secant line is a straight line that intersects a curve at two or more points. Unlike a tangent line, which touches a curve at only one point, a secant line cuts across the curve. Understanding the relationship between secant lines and tangent lines is key to understanding the concept of the derivative. The slope of a secant line represents the average rate of change of the function between the two points of intersection. As the two points get closer together, the secant line approaches the tangent line, and its slope approaches the instantaneous rate of change (the derivative).
Finding the Equation of a Secant Line: A Step-by-Step Approach
To find the equation of a secant line, you need two points on the curve. Let's denote these points as (x₁ , y₁) and (x₂, y₂). Remember that these points lie on the curve, meaning their coordinates satisfy the equation of the curve.
Here's the step-by-step process:
Step 1: Identify the two points on the curve. This might be given directly in the problem, or you may need to find them by substituting values of x into the equation of the curve to obtain the corresponding y values.
Step 2: Calculate the slope (m) of the secant line. The slope of a line passing through two points (x₁ , y₁) and (x₂, y₂) is given by the formula:
m = (y₂ - y₁) / (x₂ - x₁)
This formula represents the average rate of change of the function between the two points. A positive slope indicates an increasing function between those points, while a negative slope indicates a decreasing function.
Step 3: Use the point-slope form of a linear equation. Once you have the slope, you can use the point-slope form of a linear equation to find the equation of the secant line. The point-slope form is:
y - y₁ = m(x - x₁)
Here, m is the slope calculated in Step 2, and (x₁, y₁) is one of the two points on the curve. You can use either point; the resulting equation will be the same.
Step 4: Simplify the equation. After substituting the values of m and (x₁, y₁), simplify the equation to the slope-intercept form (y = mx + b) or the standard form (Ax + By = C), depending on the requirements of the problem.
Examples: Finding the Equation of a Secant Line
Let's illustrate this with a few examples:
Example 1: Finding the Secant Line for a Simple Function
Let's consider the function f(x) = x² + 2. Let's find the equation of the secant line that passes through the points (1, 3) and (3, 11) on the curve.
-
Points: (1, 3) and (3, 11) are given.
-
Slope: m = (11 - 3) / (3 - 1) = 8 / 2 = 4
-
Point-slope form: Using point (1, 3), we get: y - 3 = 4(x - 1)
-
Simplified equation: y = 4x - 1
Example 2: Finding the Secant Line when Points Aren't Explicitly Given
Consider the function g(x) = x³ - 2x. Find the equation of the secant line between x = 1 and x = 3.
-
Points: First, we need to find the y-coordinates for x = 1 and x = 3:
- For x = 1: g(1) = 1³ - 2(1) = -1. So, point (1, -1).
- For x = 3: g(3) = 3³ - 2(3) = 27 - 6 = 21. So, point (3, 21).
-
Slope: m = (21 - (-1)) / (3 - 1) = 22 / 2 = 11
-
Point-slope form: Using point (1, -1), we have: y - (-1) = 11(x - 1)
-
Simplified equation: y = 11x - 12
Example 3: Secant Line for a More Complex Function
Let's find the equation of the secant line for the function h(x) = √x between x = 1 and x = 4.
-
Points:
- For x = 1: h(1) = √1 = 1. Point (1, 1)
- For x = 4: h(4) = √4 = 2. Point (4, 2)
-
Slope: m = (2 - 1) / (4 - 1) = 1/3
-
Point-slope form: Using (1, 1): y - 1 = (1/3)(x - 1)
-
Simplified equation: y = (1/3)x + 2/3
Applications of Secant Lines
The concept of a secant line has significant applications in various areas, including:
-
Calculus: As mentioned earlier, understanding secant lines is crucial for understanding the concept of the derivative and instantaneous rates of change. The slope of the secant line gives the average rate of change, which converges to the instantaneous rate of change as the two points approach each other. This forms the basis for understanding derivatives and their applications in optimization, modeling, and more.
-
Numerical Analysis: Secant lines are used in numerical methods to approximate the roots of equations (the Secant Method). This iterative method refines the approximation by repeatedly finding the intersection of secant lines.
-
Physics: The average velocity of an object over a time interval can be represented by the slope of the secant line on a position-time graph.
-
Economics: Secant lines can be used to analyze the average rate of change in economic variables, such as production costs, consumer demand, and market trends.
Tips and Considerations
-
Accuracy: Be meticulous in your calculations, particularly when dealing with fractions or decimals, to minimize errors.
-
Choosing Points: When points are not given explicitly, choose points that are easy to calculate and that clearly illustrate the behavior of the function between those points.
-
Visualization: Sketching the graph of the function and the secant line can be extremely helpful in understanding the problem and verifying your answer.
-
Software Tools: Consider using graphing calculators or software like GeoGebra or Desmos to visualize the function and the secant line to confirm your calculations.
Conclusion
Finding the equation of a secant line is a fundamental skill in mathematics with widespread applications. By following the steps outlined in this guide and practicing with various examples, you can master this skill and build a strong foundation for more advanced mathematical concepts. Remember that understanding the average rate of change represented by the slope is crucial to grasping the underlying concept. This understanding lays the groundwork for the more sophisticated concept of instantaneous rate of change, which is the core of differential calculus. Keep practicing, and you'll be solving secant line problems like a pro in no time!
Latest Posts
Latest Posts
-
What Percent Of 36 Is 45
Mar 31, 2025
-
14 Is 70 Of What Number
Mar 31, 2025
-
What Is Half Of 1 1 3 Cup In Cooking
Mar 31, 2025
-
3 And 1 2 As An Improper Fraction
Mar 31, 2025
-
What Is 60 Percent Of 200
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about How Do You Find The Equation Of A Secant Line . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
