How Do You Factor 3x 2 5x 2
listenit
Mar 29, 2025 · 5 min read
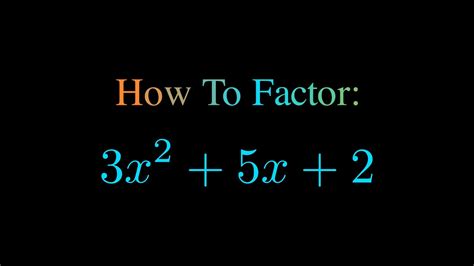
Table of Contents
How Do You Factor 3x² + 5x + 2? A Comprehensive Guide to Quadratic Factoring
Factoring quadratic expressions is a fundamental skill in algebra. Understanding how to factor these expressions opens doors to solving quadratic equations, simplifying complex algebraic expressions, and tackling more advanced mathematical concepts. This comprehensive guide will delve into the process of factoring the quadratic expression 3x² + 5x + 2, exploring various methods and providing a thorough understanding of the underlying principles.
Understanding Quadratic Expressions
Before we dive into factoring 3x² + 5x + 2, let's establish a basic understanding of quadratic expressions. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (in this case, x) is 2. It generally takes the form ax² + bx + c, where a, b, and c are constants, and a ≠ 0. In our example, 3x² + 5x + 2, a = 3, b = 5, and c = 2.
Method 1: AC Method (Factoring by Grouping)
The AC method, also known as factoring by grouping, is a widely used technique for factoring quadratic expressions where the leading coefficient (a) is not equal to 1. Here's how it works for 3x² + 5x + 2:
-
Find the product AC: Multiply the coefficient of the x² term (a) by the constant term (c): 3 * 2 = 6.
-
Find two numbers that add up to B and multiply to AC: We need to find two numbers that add up to 5 (the coefficient of the x term, b) and multiply to 6. These numbers are 3 and 2 (3 + 2 = 5 and 3 * 2 = 6).
-
Rewrite the middle term: Rewrite the middle term (5x) as the sum of the two numbers we found, multiplied by x: 3x + 2x. This gives us: 3x² + 3x + 2x + 2.
-
Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair:
- Group 1: 3x² + 3x. The GCF is 3x, so we get: 3x(x + 1).
- Group 2: 2x + 2. The GCF is 2, so we get: 2(x + 1).
-
Factor out the common binomial: Notice that both terms now share the common binomial (x + 1). Factor this out: (x + 1)(3x + 2).
Therefore, the factored form of 3x² + 5x + 2 is (x + 1)(3x + 2).
Method 2: Trial and Error
The trial and error method involves systematically testing different combinations of binomial factors until you find the pair that expands to the original quadratic expression. This method is often faster for simpler quadratics but can become more time-consuming with larger coefficients.
For 3x² + 5x + 2, we know that the factors will be of the form (ax + b)(cx + d), where a, b, c, and d are integers. Since the coefficient of x² is 3, the only integer factor pairs are (3,1) and (-3,-1). The constant term is 2, so the integer factor pairs are (2,1), (1,2), (-2,-1), (-1,-2).
We can test different combinations:
- (3x + 1)(x + 2) = 3x² + 7x + 2 (Incorrect)
- (3x + 2)(x + 1) = 3x² + 5x + 2 (Correct!)
Therefore, the factored form of 3x² + 5x + 2 is again (x + 1)(3x + 2).
Method 3: Using the Quadratic Formula (Indirect Factoring)
While not a direct factoring method, the quadratic formula can be used to find the roots of the quadratic equation 3x² + 5x + 2 = 0. These roots can then be used to construct the factored form.
The quadratic formula is: x = [-b ± √(b² - 4ac)] / 2a
For 3x² + 5x + 2 = 0, a = 3, b = 5, and c = 2. Substituting these values into the quadratic formula:
x = [-5 ± √(5² - 4 * 3 * 2)] / (2 * 3) x = [-5 ± √(25 - 24)] / 6 x = [-5 ± √1] / 6 x = (-5 ± 1) / 6
This gives us two roots:
- x₁ = (-5 + 1) / 6 = -4/6 = -2/3
- x₂ = (-5 - 1) / 6 = -6/6 = -1
The factored form is given by a(x - x₁)(x - x₂), where a is the leading coefficient. Therefore:
3(x - (-2/3))(x - (-1)) = 3(x + 2/3)(x + 1) = (3x + 2)(x + 1)
This confirms the factored form is (x + 1)(3x + 2).
Checking Your Answer
It's crucial to always check your answer by expanding the factored form. Expanding (x + 1)(3x + 2) using the FOIL method (First, Outer, Inner, Last):
- First: x * 3x = 3x²
- Outer: x * 2 = 2x
- Inner: 1 * 3x = 3x
- Last: 1 * 2 = 2
Adding these terms together: 3x² + 2x + 3x + 2 = 3x² + 5x + 2. This matches our original quadratic expression, confirming the factoring is correct.
Applications of Factoring Quadratic Expressions
The ability to factor quadratic expressions is essential in many areas of mathematics and beyond:
-
Solving Quadratic Equations: Factoring allows you to easily find the roots (solutions) of quadratic equations. Setting each factor to zero and solving for x gives the solutions.
-
Simplifying Algebraic Expressions: Factoring simplifies complex algebraic expressions, making them easier to manipulate and understand.
-
Calculus: Factoring plays a crucial role in calculus, especially when dealing with derivatives, integrals, and limits.
-
Physics and Engineering: Quadratic equations and their solutions are fundamental in modeling many physical phenomena, including projectile motion, oscillations, and circuit analysis.
Conclusion: Mastering Quadratic Factoring
Factoring the quadratic expression 3x² + 5x + 2, as demonstrated through the AC method, trial and error, and indirectly via the quadratic formula, highlights the versatility and importance of this algebraic skill. Choosing the best method depends on personal preference and the complexity of the quadratic expression. Practice is key to mastering these techniques and building a strong foundation in algebra. Remember to always check your answer by expanding the factored form to ensure accuracy. The ability to factor efficiently and accurately is a cornerstone of success in higher-level mathematics and related fields. By understanding the underlying principles and practicing regularly, you'll become proficient in this crucial algebraic skill.
Latest Posts
Latest Posts
-
What Is The Name Of The Compound Hbr
Mar 31, 2025
-
What Percent Of 36 Is 45
Mar 31, 2025
-
14 Is 70 Of What Number
Mar 31, 2025
-
What Is Half Of 1 1 3 Cup In Cooking
Mar 31, 2025
-
3 And 1 2 As An Improper Fraction
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about How Do You Factor 3x 2 5x 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
