What Is The Sum Of A Heptagons Interior Angles
listenit
Mar 31, 2025 · 5 min read
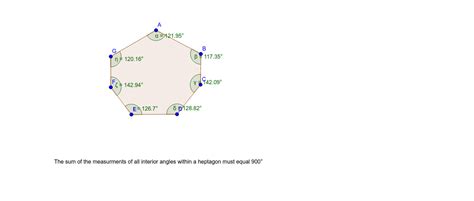
Table of Contents
What is the Sum of a Heptagon's Interior Angles? A Comprehensive Guide
The question, "What is the sum of a heptagon's interior angles?" might seem simple at first glance. However, understanding the underlying principles behind calculating interior angles of polygons, particularly irregular ones, provides valuable insights into geometry and problem-solving. This comprehensive guide will delve deep into this question, exploring various approaches, providing examples, and extending the concept to other polygons.
Understanding Polygons and Their Angles
Before we tackle heptagons specifically, let's establish a foundational understanding of polygons. A polygon is a two-dimensional closed figure formed by connecting three or more straight line segments. These segments are called the polygon's sides, and the points where the sides meet are called vertices. Polygons are classified based on the number of sides they have:
- Triangle: 3 sides
- Quadrilateral: 4 sides
- Pentagon: 5 sides
- Hexagon: 6 sides
- Heptagon (or Septagon): 7 sides
- Octagon: 8 sides
- Nonagon: 9 sides
- Decagon: 10 sides
- And so on...
Each polygon possesses both interior angles (the angles formed inside the polygon by its sides) and exterior angles (the angles formed by extending one side of the polygon and the adjacent side). The sum of these angles is governed by specific mathematical rules.
Calculating the Sum of Interior Angles: The Formula
The most efficient way to calculate the sum of a polygon's interior angles is through a formula. This formula elegantly relates the number of sides of a polygon to the sum of its interior angles:
Sum of Interior Angles = (n - 2) * 180°
Where 'n' represents the number of sides of the polygon.
This formula works for all polygons, regardless of whether they are regular (all sides and angles are equal) or irregular (sides and angles are of different lengths and measures).
Let's apply this formula to a heptagon:
A heptagon has 7 sides, so n = 7.
Sum of Interior Angles = (7 - 2) * 180° = 5 * 180° = 900°
Therefore, the sum of the interior angles of any heptagon is always 900 degrees.
Understanding the Formula's Derivation
The formula (n - 2) * 180° isn't arbitrarily chosen. It's derived from a fundamental geometric principle: triangulation. Any polygon can be divided into triangles by drawing diagonals from one vertex to all other non-adjacent vertices. The number of triangles formed is always two less than the number of sides (n - 2). Since the sum of the angles in a triangle is always 180°, the total sum of the interior angles of the polygon is simply the number of triangles multiplied by 180°.
Heptagons: Regular vs. Irregular
The formula applies equally to both regular and irregular heptagons.
-
Regular Heptagon: A regular heptagon has all sides of equal length and all interior angles of equal measure. Each interior angle of a regular heptagon measures 900°/7 ≈ 128.57°.
-
Irregular Heptagon: An irregular heptagon has sides and angles of varying lengths and measures. The sum of its interior angles remains 900°, but the individual angles will differ.
Practical Applications and Examples
Understanding the sum of interior angles has practical applications in various fields, including:
-
Architecture: Architects use geometric principles to design buildings and structures. Knowing the angle sums helps in creating stable and aesthetically pleasing designs. For example, designing a seven-sided gazebo requires precise angle calculations to ensure structural integrity.
-
Engineering: Engineers use geometric calculations in designing mechanical parts and systems. Precise angular measurements are critical in many engineering applications.
-
Computer Graphics: In computer graphics and game development, polygon modeling is extensively used. Accurate calculation of interior angles is essential for creating realistic and accurate 3D models.
-
Cartography: Mapmaking involves geometric projections and calculations. Understanding polygon angles is crucial for creating accurate maps.
Example 1: Finding a Missing Angle
Let's say we have an irregular heptagon where six of the angles are known: 130°, 115°, 140°, 125°, 150°, and 100°. To find the missing angle (let's call it x), we can use the formula:
900° = 130° + 115° + 140° + 125° + 150° + 100° + x
Solving for x:
x = 900° - (130° + 115° + 140° + 125° + 150° + 100°) = 900° - 760° = 140°
The missing angle is 140°.
Example 2: Designing a Heptagonal Table
Imagine designing a seven-sided table. To ensure the table's top is a true heptagon, you need to precisely calculate each angle. While a perfectly regular heptagon might be challenging to construct, understanding the 900° total ensures that the angles sum correctly, even if it's an irregular design.
Extending the Concept to Other Polygons
The formula (n - 2) * 180° is a powerful tool applicable to all polygons. Let's consider a few examples:
-
Triangle (n = 3): (3 - 2) * 180° = 180° (The well-known sum of angles in a triangle)
-
Quadrilateral (n = 4): (4 - 2) * 180° = 360°
-
Pentagon (n = 5): (5 - 2) * 180° = 540°
-
Hexagon (n = 6): (6 - 2) * 180° = 720°
-
Octagon (n = 8): (8 - 2) * 180° = 1080°
Conclusion: The Significance of Understanding Polygon Angles
Understanding how to calculate the sum of interior angles of polygons, and specifically the heptagon's 900° sum, is crucial in various fields. This knowledge is not just a theoretical concept; it's a practical tool used in design, engineering, computer graphics, and many other areas. By grasping the formula and its derivation, we gain a deeper appreciation of geometry and its applications in the real world. The ability to solve problems involving polygon angles enhances problem-solving skills and fosters a stronger understanding of mathematical principles. Remember, this knowledge extends beyond heptagons to all polygons, showcasing the elegance and power of geometric formulas.
Latest Posts
Latest Posts
-
How To Find The Secant Line
Apr 01, 2025
-
What Is 2 To The Fifth Power
Apr 01, 2025
-
How Many Electrons Can The First Shell Hold
Apr 01, 2025
-
15 6 As A Mixed Number
Apr 01, 2025
-
What Two Monosaccharides Make Up Sucrose
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is The Sum Of A Heptagons Interior Angles . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
