15 6 As A Mixed Number
listenit
Apr 01, 2025 · 5 min read
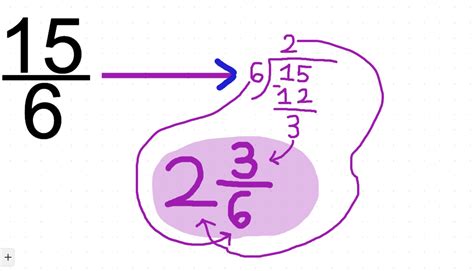
Table of Contents
- 15 6 As A Mixed Number
- Table of Contents
- 15/6 as a Mixed Number: A Comprehensive Guide
- What is a Mixed Number?
- What is an Improper Fraction?
- Converting 15/6 to a Mixed Number: Step-by-Step Guide
- Simplifying the Fraction
- Visual Representation of 15/6
- Real-World Applications of Mixed Numbers
- Working with Mixed Numbers: Addition, Subtraction, Multiplication, and Division
- Importance of Understanding Fractions and Mixed Numbers
- Beyond 15/6: Practicing with Other Improper Fractions
- Conclusion: Mastering Mixed Numbers
- Latest Posts
- Latest Posts
- Related Post
15/6 as a Mixed Number: A Comprehensive Guide
Understanding fractions and how to convert them into mixed numbers is a fundamental skill in mathematics. This comprehensive guide will delve into the process of converting the improper fraction 15/6 into a mixed number, explaining the concepts involved in detail and providing practical examples. We'll also explore the broader context of fractions and mixed numbers, highlighting their importance in various applications.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is one where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 2 ¾ is a mixed number; it represents two whole units and three-quarters of another unit.
What is an Improper Fraction?
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. The fraction 15/6 is an improper fraction because the numerator (15) is larger than the denominator (6). Improper fractions represent values greater than or equal to one.
Converting 15/6 to a Mixed Number: Step-by-Step Guide
The process of converting an improper fraction like 15/6 to a mixed number involves dividing the numerator by the denominator. Here's a step-by-step breakdown:
-
Divide the Numerator by the Denominator: Divide 15 by 6. This gives you a quotient (the result of the division) and a remainder.
15 ÷ 6 = 2 with a remainder of 3
-
Identify the Whole Number: The quotient (2) becomes the whole number part of your mixed number.
-
Identify the New Numerator: The remainder (3) becomes the numerator of the fractional part of your mixed number.
-
Keep the Original Denominator: The denominator (6) remains the same in the fractional part of your mixed number.
-
Combine the Whole Number and Fraction: Combine the whole number and the fraction to form the mixed number.
Therefore, 15/6 = 2 3/6
Simplifying the Fraction
Notice that the fraction part of our mixed number, 3/6, can be simplified. Both the numerator and denominator are divisible by 3.
3 ÷ 3 = 1 6 ÷ 3 = 2
So, 3/6 simplifies to 1/2.
Therefore, the simplified mixed number representation of 15/6 is 2 ½.
Visual Representation of 15/6
Imagine you have 15 equally sized pieces of pizza. If each person gets 6 pieces, you can feed 2 people completely (that's your whole number, 2). You'll have 3 pieces left over (the remainder), which is 3 out of 6 pieces (3/6 or ½). This visually demonstrates the mixed number 2 ½.
Real-World Applications of Mixed Numbers
Mixed numbers are used extensively in everyday life and across various fields. Here are a few examples:
-
Cooking: Recipes often call for mixed numbers, like 2 ½ cups of flour or 1 ¼ teaspoons of baking powder.
-
Measurements: Measuring lengths, weights, and volumes frequently involves mixed numbers. You might measure a piece of wood as 2 3/8 feet long.
-
Time: Telling time involves understanding and using fractions and mixed numbers. For example, 2 hours and 15 minutes can be represented as 2 ¼ hours.
-
Construction: In construction and engineering, precise measurements are critical, and mixed numbers are used for accuracy.
-
Finance: Financial calculations may involve fractions and mixed numbers for representing shares of stock or portions of interest rates.
Working with Mixed Numbers: Addition, Subtraction, Multiplication, and Division
Once you understand mixed numbers, you'll need to know how to perform basic arithmetic operations with them. It's often easier to convert mixed numbers to improper fractions before performing these calculations, then converting the result back to a mixed number if needed.
Addition and Subtraction:
To add or subtract mixed numbers, you can either:
-
Convert to Improper Fractions: Convert each mixed number to an improper fraction, then perform the addition or subtraction. Finally, convert the result back to a mixed number if it's improper.
-
Add/Subtract Whole Numbers and Fractions Separately: Add or subtract the whole numbers and the fractions separately. If the fraction part results in an improper fraction, convert it to a mixed number and add it to the whole number part.
Multiplication and Division:
For multiplication and division, it's generally easier to:
- Convert to Improper Fractions: Convert each mixed number to an improper fraction, then perform the multiplication or division. Convert the result back to a mixed number if necessary.
Importance of Understanding Fractions and Mixed Numbers
A solid understanding of fractions and mixed numbers is crucial for success in various areas of life, including:
-
Academic Achievement: Mastering fractions is essential for success in mathematics and related subjects like science and engineering.
-
Problem-Solving Skills: Working with fractions helps develop critical thinking and problem-solving skills.
-
Everyday Life: As demonstrated earlier, fractions and mixed numbers are applied extensively in daily routines.
-
Career Opportunities: Many careers require a strong understanding of fractions and mathematical concepts.
Beyond 15/6: Practicing with Other Improper Fractions
To solidify your understanding, practice converting other improper fractions to mixed numbers. Try these examples:
- 22/7
- 17/5
- 31/8
- 45/12
Remember to always simplify the resulting fractions when possible.
Conclusion: Mastering Mixed Numbers
Converting 15/6 to a mixed number, and understanding the broader concept of mixed numbers, is an essential mathematical skill. This comprehensive guide has provided a step-by-step approach, real-world examples, and practice problems to help you master this fundamental concept. With consistent practice, you’ll confidently navigate fractions and mixed numbers in all your academic and real-world endeavors. Remember that understanding the underlying principles—division, remainders, and fraction simplification—will help you succeed in more complex mathematical scenarios. Practice regularly, and soon you'll find yourself effortlessly converting improper fractions into their equivalent mixed number representations.
Latest Posts
Latest Posts
-
Water Is Made Up Of Which Two Elements
Apr 04, 2025
-
What Is 9 Percent Of 50
Apr 04, 2025
-
Distance From Earth To Pluto In Light Years
Apr 04, 2025
-
Molar Mass Of Copper 2 Sulfate
Apr 04, 2025
-
Common Multiples Of 9 And 6
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about 15 6 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
