What Is The Square Root Of 240
listenit
Apr 03, 2025 · 5 min read
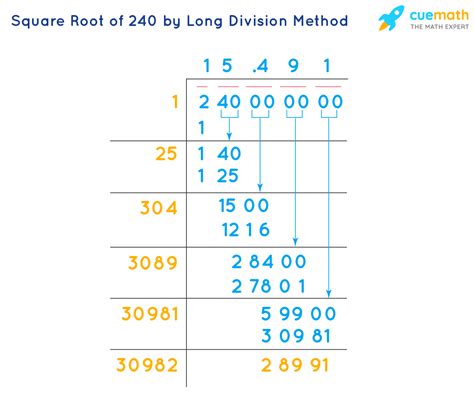
Table of Contents
What is the Square Root of 240? A Deep Dive into Square Roots and Their Applications
The seemingly simple question, "What is the square root of 240?" opens a door to a fascinating world of mathematics, encompassing fundamental concepts, practical applications, and even historical significance. While a calculator quickly provides an approximate decimal answer, understanding the process and implications goes far beyond a simple numerical result. This article will delve into the square root of 240, exploring its calculation, its properties, and its relevance in various fields.
Understanding Square Roots
Before tackling the square root of 240 specifically, let's establish a solid foundation in the concept of square roots. The square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 is 3, because 3 x 3 = 9. This is often represented mathematically as √9 = 3.
The square root operation is the inverse of squaring a number. Squaring a number means multiplying it by itself (e.g., 5² = 5 x 5 = 25). Therefore, finding the square root is essentially asking, "What number, when multiplied by itself, gives me this value?"
Calculating the Square Root of 240
Unlike perfect squares (numbers like 9, 16, 25, etc., which have whole number square roots), 240 does not have a whole number square root. This means its square root is an irrational number – a number that cannot be expressed as a simple fraction. It has an infinite number of decimal places and doesn't repeat in a predictable pattern.
Methods for Calculating:
-
Calculator: The simplest method is using a calculator. Most calculators have a square root function (√). Simply enter 240 and press the square root button. The result will be approximately 15.4919333848.
-
Approximation by Estimation: Without a calculator, we can estimate the square root. We know that 15² = 225 and 16² = 256. Since 240 falls between 225 and 256, its square root must be between 15 and 16. A closer estimation can be achieved by considering the proximity of 240 to 225 and 256.
-
Babylonian Method (or Heron's Method): This iterative method provides increasingly accurate approximations. Start with an initial guess (e.g., 15). Then, repeatedly apply the formula:
x_(n+1) = 0.5 * (x_n + (N / x_n))where:
x_nis the current guessNis the number (240 in our case)x_(n+1)is the next guess
Repeating this process several times will converge towards the accurate square root.
-
Prime Factorization: While not directly yielding the decimal value, prime factorization helps understand the structure of the number. 240 can be factorized as 2⁴ x 3 x 5. This factorization is useful in simplifying square roots of larger numbers but doesn't directly provide the square root of 240 in its decimal form. It can be simplified as follows: √240 = √(2⁴ x 3 x 5) = √(16 x 15) = 4√15
Properties of the Square Root of 240
-
Irrationality: As mentioned, √240 is an irrational number. This means its decimal representation is non-terminating and non-repeating.
-
Approximation: While we can't express it exactly as a fraction or terminating decimal, we can approximate it to any desired level of accuracy using methods described above.
-
Relationship to other numbers: √240 is related to other numbers through operations like addition, subtraction, multiplication, and division. For example, it is approximately 15.5, which can be used for estimations in various calculations.
Applications of Square Roots
Square roots, and more generally, the concept of square roots have far-reaching applications across various fields:
-
Geometry: Calculating distances, areas, and volumes frequently involves square roots. For example, the Pythagorean theorem (a² + b² = c²) uses square roots to find the length of the hypotenuse of a right-angled triangle. Areas of circles (πr²) and volumes of spheres (4/3πr³) also involve square roots in calculations of radius from area or volume.
-
Physics: Many physical phenomena are modeled using square roots. For instance, calculating the velocity of an object under the influence of gravity, the period of a pendulum, or the energy levels of electrons in an atom often involve square roots. Equations involving the concept of energy (E=mc²) also demonstrate the significance of square roots in the calculations.
-
Engineering: In civil, mechanical, and electrical engineering, square roots are frequently used in calculations concerning stress, strain, impedance, and signal processing. The square root is vital in many engineering applications that require precise calculations for structural integrity, material strength and other important factors.
-
Finance: Standard deviation, a key measure of risk in finance, involves the square root of variance ( a measure of how spread out a set of numbers are).
-
Computer Science: Square root calculations are fundamental to numerous algorithms in computer graphics, simulations, and optimization problems. The efficient computation of square roots is a significant area of research in computer science.
-
Statistics: Standard deviation, as already mentioned, is crucial in statistical analysis, providing a measure of the spread or dispersion of data. Determining the confidence intervals in inferential statistics involves the square root. Many statistical computations rely heavily on the use of square roots to determine standard deviations.
Historical Context
The concept of square roots has a rich history, dating back to ancient civilizations. Babylonian mathematicians developed methods for approximating square roots thousands of years ago. The Greeks, notably Pythagoras, explored the properties of square roots and their relationship to geometry. The understanding and calculation of square roots have advanced significantly over time, leading to the sophisticated mathematical tools we use today.
Conclusion: Beyond the Number
The square root of 240, while appearing to be a simple calculation, underscores the depth and breadth of the concept of square roots. Its irrational nature highlights the complexities of numbers, while its numerous applications across various disciplines underscore its practical significance. From geometry to finance, from physics to computer science, understanding square roots provides valuable insights into the world around us and allows us to engage with complex mathematical models. The seemingly straightforward number 15.4919... becomes a gateway to a wider appreciation of mathematics and its power to shape our understanding of the universe.
Latest Posts
Latest Posts
-
What Is 3 And 1 2 As A Decimal
Apr 03, 2025
-
Which Subatomic Particle Contributes To The Mass Of An Atom
Apr 03, 2025
-
What Is The Absolute Zero On The Celsius Scale
Apr 03, 2025
-
Meaning Of Trunk In Human Body
Apr 03, 2025
-
How Many Valence Electrons Are In Ar
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of 240 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
