Which Subatomic Particle Contributes To The Mass Of An Atom
listenit
Apr 03, 2025 · 5 min read
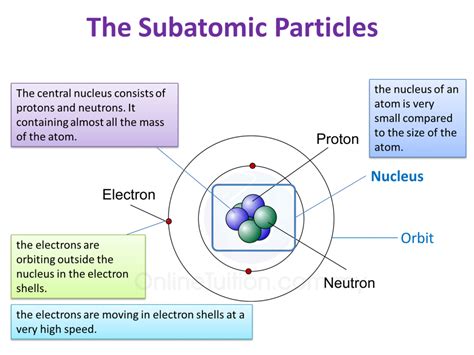
Table of Contents
Which Subatomic Particle Contributes to the Mass of an Atom?
The question of which subatomic particle contributes to the mass of an atom is a fundamental one in physics, seemingly simple yet rich in nuance. While the answer is straightforward at a basic level, a deeper dive reveals fascinating intricacies and subtleties related to the complexities of quantum mechanics and Einstein's famous equation, E=mc². This article will explore this question comprehensively, moving from the simple to the more advanced concepts.
The Simple Answer: Protons and Neutrons
At the most basic level, the answer is clear: protons and neutrons are the primary contributors to an atom's mass. Electrons, the third major subatomic particle, possess a mass so minuscule compared to protons and neutrons that it’s often considered negligible in the context of an atom's overall mass.
Let's put some numbers to this:
- Proton: Approximately 1.6726 × 10⁻²⁷ kg
- Neutron: Approximately 1.6749 × 10⁻²⁷ kg
- Electron: Approximately 9.1094 × 10⁻³¹ kg
Notice the significant difference in mass between electrons and the other two. The mass of an electron is roughly 1/1836th the mass of a proton. Therefore, when calculating the mass of an atom, the contribution of electrons is often disregarded.
This simple answer, however, is a starting point for a deeper understanding.
Delving Deeper: The Role of Binding Energy
While protons and neutrons are the dominant contributors to an atom's mass, the picture isn't entirely complete without considering binding energy. This energy is the force that holds the protons and neutrons together in the atom's nucleus. Einstein's famous equation, E=mc², reveals a crucial connection between energy and mass. This equation states that energy and mass are interchangeable, and a change in one will cause a change in the other.
In the nucleus, the strong nuclear force overcomes the electromagnetic repulsion between positively charged protons. This strong force is associated with a significant amount of energy. Because of E=mc², this binding energy translates to a decrease in the atom's mass. In other words, the mass of the nucleus is slightly less than the sum of the masses of its constituent protons and neutrons in isolation. This mass difference is known as the mass defect.
The mass defect is a direct consequence of the strong nuclear force and is a crucial factor in nuclear reactions, such as nuclear fission and fusion. A significant amount of energy is released during these reactions because the mass defect is converted into energy, as described by E=mc².
This subtle effect demonstrates that the mass of an atom isn't just the simple sum of its proton and neutron masses; it also accounts for the energy binding the nucleus together.
Isotopes and Atomic Mass: A Deeper Dive into Mass Variation
Atoms of the same element can have different numbers of neutrons. These variations are called isotopes. Isotopes of an element have the same number of protons (which defines the element), but different numbers of neutrons. This difference in neutron number directly impacts the atom's mass.
For instance, carbon-12 (¹²C) has 6 protons and 6 neutrons, while carbon-14 (¹⁴C) has 6 protons and 8 neutrons. ¹⁴C is heavier than ¹²C because it has two extra neutrons. This difference, though seemingly small at the atomic level, is significant when considering large quantities of atoms.
The atomic mass of an element reported on the periodic table represents a weighted average of the masses of all its naturally occurring isotopes, taking into account their relative abundances. This means the atomic mass doesn't represent the mass of a single atom but rather a statistical average mass.
The Insignificant Mass of Electrons: A Closer Look
While we've repeatedly stated that the electron's mass is negligible, it's important to understand why this is the case. The incredibly small mass of electrons arises from their fundamental nature as elementary particles. Unlike protons and neutrons, which are composed of quarks, electrons are considered fundamental particles – meaning they are not made up of smaller constituents (at least as far as our current understanding goes). Their relatively small mass is an intrinsic property.
Relativistic Effects and Mass-Energy Equivalence: Advanced Considerations
At very high energies, such as those encountered in particle accelerators, relativistic effects become significant. Einstein's theory of special relativity demonstrates that the mass of a particle increases with its velocity. This relativistic mass increase is described by the equation:
m = m₀ / √(1 - v²/c²)
Where:
- m is the relativistic mass
- m₀ is the rest mass
- v is the velocity of the particle
- c is the speed of light
While this effect is negligible at everyday speeds, it becomes crucial at speeds approaching the speed of light. This means that even the mass of electrons can become non-negligible at extremely high velocities. This is another layer of complexity that shows how the "simple" answer about protons and neutrons being the primary mass contributors requires careful consideration of the context.
Beyond Protons and Neutrons: The Quark Contribution
Protons and neutrons themselves are not fundamental particles. They are composed of even smaller particles called quarks. Each proton and neutron contains three quarks held together by the strong nuclear force. The mass of a proton or neutron is largely determined by the mass of its constituent quarks and the energy binding them together. This binding energy, again, plays a significant role. The interaction energy between quarks is even more significant than the rest mass of the quarks themselves! The majority of the mass of protons and neutrons comes from the energy of the strong force field that holds the quarks together.
Conclusion: A Holistic View of Atomic Mass
The seemingly straightforward question of which subatomic particle contributes to an atom's mass reveals a rich tapestry of concepts from classical and modern physics. While protons and neutrons are the primary contributors, the nuances of binding energy, isotopic variations, relativistic effects, and the underlying quark structure significantly refine our understanding. The mass of an atom isn't a simple sum but a complex interplay of the masses of its constituents and the powerful forces that bind them together, all deeply connected through Einstein's revolutionary equation, E=mc². Understanding this holistic view is crucial for a complete grasp of atomic structure and nuclear physics.
Latest Posts
Latest Posts
-
Is Black Coffee A Homogeneous Mixture
Apr 04, 2025
-
A Column On The Periodic Table Is Called A
Apr 04, 2025
-
What Is The Oxidation Number Of Na
Apr 04, 2025
-
How To Write 80 As A Fraction
Apr 04, 2025
-
Write The Equation Of The Function Whose Graph Is Shown
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Which Subatomic Particle Contributes To The Mass Of An Atom . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
