What Is The Square Root Of 145
listenit
Mar 17, 2025 · 4 min read
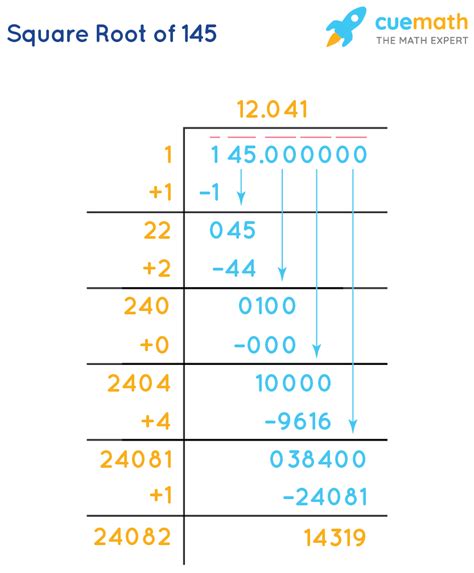
Table of Contents
What is the Square Root of 145? A Deep Dive into Square Roots and Approximations
The question, "What is the square root of 145?" might seem simple at first glance. However, exploring this seemingly straightforward mathematical problem opens doors to a fascinating world of numerical analysis, approximation techniques, and the deeper understanding of irrational numbers. Let's delve into this seemingly simple question and uncover its complexities.
Understanding Square Roots
Before we tackle the square root of 145 specifically, let's establish a foundational understanding of what a square root actually represents. The square root of a number, denoted by the symbol √, is a value that, when multiplied by itself, equals the original number. For example:
- √9 = 3 because 3 * 3 = 9
- √16 = 4 because 4 * 4 = 16
- √25 = 5 because 5 * 5 = 25
This concept is straightforward for perfect squares – numbers that result from squaring whole numbers. However, the square root of 145 presents a unique challenge because 145 is not a perfect square. This means its square root is an irrational number – a number that cannot be expressed as a simple fraction and its decimal representation continues infinitely without repeating.
Calculating the Square Root of 145: Methods and Techniques
There are several ways to approach finding the square root of 145:
1. Using a Calculator
The simplest method is using a calculator. Most scientific calculators have a square root function (√) that will directly provide an approximate value. Using a calculator, we find that:
√145 ≈ 12.0415945788
This is an approximation, as the actual value has infinitely many decimal places.
2. Babylonian Method (or Heron's Method)
This ancient iterative method provides a way to approximate square roots. It involves repeatedly refining an initial guess until the desired level of accuracy is achieved. The formula is:
x_(n+1) = 0.5 * (x_n + (N / x_n))
Where:
x_nis the current approximationNis the number whose square root we are seeking (145 in our case)x_(n+1)is the improved approximation
Let's demonstrate with an initial guess of 12:
- Iteration 1: x₁ = 0.5 * (12 + (145 / 12)) ≈ 12.041666...
- Iteration 2: x₂ = 0.5 * (12.041666... + (145 / 12.041666...)) ≈ 12.0415945788
As you can see, even after just two iterations, we reach a very close approximation to the calculator's result. Further iterations would yield even greater precision.
3. Prime Factorization and Simplification
While 145 is not a perfect square, we can try to simplify the square root using prime factorization. The prime factorization of 145 is 5 x 29. Since there are no repeated prime factors, the square root cannot be simplified further. Therefore, √145 remains as it is.
4. Linear Approximation
A simple linear approximation can be made by identifying the nearest perfect squares:
- 12² = 144
- 13² = 169
Since 145 is closer to 144 than 169, a rough estimate would be slightly above 12. This method lacks precision but provides a quick, albeit crude, approximation.
The Significance of Irrational Numbers: √145 as an Example
The fact that √145 is irrational highlights a fundamental aspect of mathematics. Not all numbers can be neatly expressed as fractions or terminating decimals. Irrational numbers, like π (pi) and e (Euler's number), play crucial roles in various mathematical and scientific fields.
The inability to express √145 exactly as a decimal underscores the importance of approximation techniques. These techniques are essential for solving real-world problems where precise, analytical solutions are often impractical or impossible.
Applications and Real-World Examples
While the square root of 145 might seem like a purely abstract concept, it has real-world applications, albeit often indirectly. For instance:
- Geometry: Calculating the diagonal of a rectangle or the hypotenuse of a right-angled triangle might involve a square root of a non-perfect square, leading to an irrational value.
- Physics: Many physical phenomena involve irrational numbers. For example, calculations involving oscillations, wave propagation, or projectile motion might necessitate working with irrational numbers.
- Engineering: Architectural design, civil engineering, and other engineering disciplines often use geometry and trigonometry, leading to calculations involving irrational numbers.
- Computer Graphics: Creating realistic images and animations relies on mathematical calculations, many of which involve irrational numbers.
Conclusion: Embracing the Beauty of Approximation
In conclusion, finding the square root of 145 isn't just about obtaining a numerical answer. It's about understanding the nature of irrational numbers, exploring different approximation methods, and appreciating the practical significance of these seemingly abstract mathematical concepts. Whether you use a calculator for a quick approximation or employ a more sophisticated method like the Babylonian method, remember that the true value of √145 remains an endlessly fascinating and slightly elusive target – a testament to the richness and complexity of the mathematical world. The pursuit of precision, and the acceptance of the inherent limitations in obtaining it, are both valuable lessons learned when dealing with irrational numbers like √145.
Latest Posts
Latest Posts
-
Can Acids Or Bases Conduct Electricity
Mar 17, 2025
-
How Many Valence Electros In Hydrogen
Mar 17, 2025
-
How Do Animals Get The Nitrogen They Need
Mar 17, 2025
-
Nucleotides Are Attached By Bonds Between The
Mar 17, 2025
-
The Sum Of A Number And Four
Mar 17, 2025
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of 145 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
