What Is The Graph Of A Quadratic Function Called
listenit
Mar 30, 2025 · 5 min read
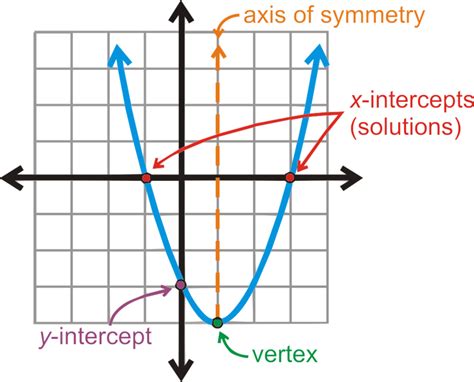
Table of Contents
What is the Graph of a Quadratic Function Called? A Deep Dive into Parabolas
The graph of a quadratic function, a polynomial function of degree two, is universally known as a parabola. Understanding parabolas is fundamental to grasping many aspects of mathematics, physics, and even engineering. This comprehensive guide delves into the intricacies of parabolas, exploring their properties, equations, and real-world applications. We'll move beyond simply defining the shape and investigate the nuances that make parabolas such a significant concept.
Understanding the Quadratic Function
Before diving into the specifics of parabolas, let's solidify our understanding of the quadratic function itself. A quadratic function is a function of the form:
f(x) = ax² + bx + c
where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero (if a=0, the function becomes linear, not quadratic). The variable 'x' represents the independent variable, and 'f(x)' or 'y' represents the dependent variable. The values of 'a', 'b', and 'c' determine the specific shape and position of the parabola.
The Significance of the 'a' Coefficient
The coefficient 'a' plays a crucial role in shaping the parabola. It dictates:
-
The direction of the parabola: If 'a' is positive (a > 0), the parabola opens upwards (it's a "U" shape). If 'a' is negative (a < 0), the parabola opens downwards (it's an inverted "U" shape).
-
The width of the parabola: The absolute value of 'a' (|a|) affects the parabola's width. A larger |a| value results in a narrower parabola, while a smaller |a| value results in a wider parabola. If |a| is close to 0, the parabola becomes wider and flatter.
Key Features of a Parabola
Parabolas possess several defining characteristics:
1. Vertex
The vertex is the lowest point on a parabola that opens upwards or the highest point on a parabola that opens downwards. It represents the minimum or maximum value of the quadratic function. The x-coordinate of the vertex can be found using the formula:
x = -b / 2a
Once you have the x-coordinate, substitute it back into the quadratic equation to find the y-coordinate of the vertex.
2. Axis of Symmetry
The axis of symmetry is a vertical line that divides the parabola into two mirror-image halves. The equation of the axis of symmetry is given by:
x = -b / 2a
Notice that this is the same formula as the x-coordinate of the vertex. This is because the vertex lies on the axis of symmetry.
3. x-intercepts (Roots or Zeros)
The x-intercepts are the points where the parabola intersects the x-axis (where y = 0). These points are also known as the roots or zeros of the quadratic function. They can be found by solving the quadratic equation:
ax² + bx + c = 0
This can be done using various methods, including factoring, the quadratic formula, or completing the square. A parabola can have two, one, or zero x-intercepts.
4. y-intercept
The y-intercept is the point where the parabola intersects the y-axis (where x = 0). It can be found by substituting x = 0 into the quadratic equation:
y = c
Therefore, the y-intercept is simply the constant term 'c' in the quadratic equation.
Different Forms of Quadratic Equations
Quadratic equations can be expressed in different forms, each offering unique insights into the parabola's properties:
1. Standard Form:
This is the form we've already discussed:
f(x) = ax² + bx + c
This form is useful for easily identifying the y-intercept and determining the direction and width of the parabola.
2. Vertex Form:
The vertex form highlights the vertex coordinates (h, k):
f(x) = a(x - h)² + k
where (h, k) represents the vertex of the parabola. This form is particularly useful for quickly identifying the vertex and axis of symmetry.
3. Intercept Form (Factored Form):
The intercept form explicitly shows the x-intercepts (roots) p and q:
f(x) = a(x - p)(x - q)
This form is helpful for directly determining the x-intercepts of the parabola.
Applications of Parabolas
Parabolas are not merely abstract mathematical concepts; they have significant real-world applications across various fields:
1. Physics: Projectile Motion
The trajectory of a projectile (like a ball thrown into the air) follows a parabolic path due to the influence of gravity. Understanding parabolic motion is essential in fields like sports science, ballistics, and aerospace engineering.
2. Engineering: Antenna Design
Parabolic reflectors, shaped like parabolas, are used in satellite dishes and radar systems to focus electromagnetic waves onto a receiver or transmitter. The parabolic shape ensures efficient collection or transmission of signals.
3. Architecture: Bridges and Arches
Parabolic arches are often used in bridge construction due to their strength and efficiency in distributing weight. The shape allows for optimal load bearing and structural integrity.
4. Optics: Telescopes and Microscopes
Parabolic mirrors are used in telescopes and some microscopes to focus light and create sharp images. The parabolic shape minimizes aberrations and enhances image quality.
Beyond the Basics: More Complex Parabolas and Transformations
While the standard parabola y = x² provides a foundational understanding, it's important to grasp how transformations affect the parabola's position and orientation. These transformations include:
-
Vertical Shifts: Adding a constant 'k' to the function, y = x² + k, shifts the parabola vertically upwards (k > 0) or downwards (k < 0).
-
Horizontal Shifts: Replacing 'x' with (x - h), y = (x - h)², shifts the parabola horizontally to the right (h > 0) or to the left (h < 0).
-
Vertical Stretches/Compressions: Multiplying the function by a constant 'a', y = ax², stretches the parabola vertically (|a| > 1) or compresses it (0 < |a| < 1).
-
Reflections: Multiplying the function by -1, y = -x², reflects the parabola across the x-axis.
Understanding these transformations allows for the precise manipulation and analysis of parabolas in various contexts.
Conclusion: The Ubiquitous Parabola
The parabola, the graph of a quadratic function, is a fundamental geometric shape with widespread applications. From understanding projectile motion to designing efficient antennas, its properties are crucial across diverse scientific and engineering disciplines. By mastering the concepts presented in this article, you'll not only gain a deeper appreciation for the mathematical elegance of parabolas but also develop a crucial skillset applicable to various real-world scenarios. Remember to practice working with different forms of quadratic equations and understanding how transformations affect the parabola's shape and position. This comprehensive understanding will solidify your grasp of this vital mathematical concept.
Latest Posts
Latest Posts
-
What Is The Improper Fraction Of 2 1 4
Apr 01, 2025
-
Lewis Acid Vs Bronsted Lowry Acid
Apr 01, 2025
-
What Is Square Root Of 63
Apr 01, 2025
-
Least Common Multiple 2 And 4
Apr 01, 2025
-
How Does Igneous Rock Become Metamorphic
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is The Graph Of A Quadratic Function Called . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
