What Is The Fraction For 0.09
listenit
Mar 31, 2025 · 5 min read
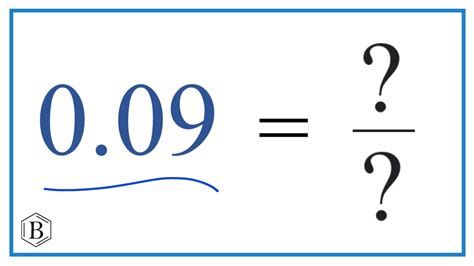
Table of Contents
What is the Fraction for 0.09? A Deep Dive into Decimal-to-Fraction Conversion
The seemingly simple question, "What is the fraction for 0.09?", opens a door to a broader understanding of decimal-to-fraction conversion, a fundamental concept in mathematics with widespread applications in various fields. This article will not only answer the question directly but also explore the underlying principles, methods, and practical implications of this conversion process. We'll delve into different approaches, address potential difficulties, and provide you with a solid grasp of this essential mathematical skill.
Understanding Decimals and Fractions
Before tackling the conversion, let's refresh our understanding of decimals and fractions.
Decimals: Decimals represent numbers less than one using a base-ten system. The digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on. For example, 0.09 represents nine hundredths.
Fractions: Fractions represent parts of a whole. They consist of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts, while the denominator indicates the total number of equal parts the whole is divided into. For example, 1/2 represents one out of two equal parts.
Converting 0.09 to a Fraction: The Straightforward Method
The most direct way to convert 0.09 to a fraction is to read the decimal aloud. 0.09 is spoken as "nine hundredths". This directly translates to the fraction 9/100.
This fraction is already in its simplest form because the greatest common divisor (GCD) of 9 and 100 is 1. Therefore, we cannot simplify it further.
Therefore, the answer to "What is the fraction for 0.09?" is 9/100.
Alternative Methods for Decimal to Fraction Conversion: A Broader Perspective
While the direct method is efficient for simple decimals like 0.09, other methods provide a more robust approach for converting more complex decimals.
Method 1: Using the Place Value
This method utilizes the place value of the last digit in the decimal. In 0.09, the last digit, 9, is in the hundredths place. This implies that the denominator of the fraction will be 100. The numerator will be the number itself (9). Hence, we get 9/100.
This method works well for terminating decimals (decimals that end).
Method 2: Writing the Decimal as a Fraction over 1
This approach involves writing the decimal as the numerator of a fraction with a denominator of 1. Then, we multiply both the numerator and denominator by a power of 10 to eliminate the decimal point.
- Write as a fraction over 1: 0.09/1
- Multiply numerator and denominator by 100: (0.09 x 100) / (1 x 100) = 9/100
This method is particularly helpful for decimals with more digits.
Method 3: Simplifying Fractions
After converting a decimal to a fraction, it's crucial to simplify the fraction to its lowest terms. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by the GCD. In the case of 9/100, the GCD is 1, meaning the fraction is already simplified.
Let's illustrate with a more complex example: converting 0.375 to a fraction.
- Write as a fraction over 1: 0.375/1
- Multiply by 1000: (0.375 x 1000) / (1 x 1000) = 375/1000
- Find the GCD of 375 and 1000: The GCD is 125.
- Simplify: 375/1000 = (375 ÷ 125) / (1000 ÷ 125) = 3/8
Therefore, 0.375 is equivalent to 3/8.
Handling Recurring Decimals (Repeating Decimals)
Recurring decimals, like 0.333... (one-third) or 0.142857142857..., present a slightly different challenge. These require a different approach than terminating decimals.
Let's illustrate with 0.333...
- Let x = 0.333...
- Multiply by 10: 10x = 3.333...
- Subtract the original equation: 10x - x = 3.333... - 0.333...
- Simplify: 9x = 3
- Solve for x: x = 3/9
- Simplify the fraction: x = 1/3
This method involves algebraic manipulation to eliminate the repeating part of the decimal. For more complex recurring decimals, the process might be more involved, but the fundamental principle remains the same.
Real-World Applications of Decimal to Fraction Conversion
The ability to convert decimals to fractions is not merely an academic exercise; it has practical applications in numerous fields:
-
Engineering and Construction: Precise measurements are crucial in these fields. Fractions often provide a more accurate representation than decimals, especially when dealing with small dimensions or tolerances.
-
Cooking and Baking: Recipes frequently call for fractional amounts of ingredients. Understanding decimal-to-fraction conversion ensures accurate measurements and successful outcomes.
-
Finance: Interest rates, stock prices, and other financial data are often expressed as decimals. Converting them to fractions can aid in calculations and comparisons.
-
Science: Scientific measurements and calculations often involve fractions, particularly in chemistry and physics. Converting decimals to fractions facilitates accurate data representation and analysis.
Addressing Common Challenges and Mistakes
Even a seemingly simple conversion can present challenges if not approached carefully. Here are some common mistakes to avoid:
-
Incorrect Simplification: Failing to simplify the fraction to its lowest terms is a common error. Always check for the GCD and simplify accordingly.
-
Misunderstanding Place Value: Incorrectly identifying the place value of the last digit in the decimal can lead to errors in determining the denominator.
-
Errors in Algebraic Manipulation (for recurring decimals): Incorrect algebraic manipulations when dealing with recurring decimals can result in an inaccurate fraction. Double-check each step to minimize errors.
Conclusion: Mastering Decimal-to-Fraction Conversion
Converting decimals to fractions is a fundamental skill with widespread applicability. While the conversion of 0.09 to 9/100 is straightforward, understanding the underlying principles and various methods enables you to tackle more complex conversions with confidence. Mastering this skill enhances your mathematical proficiency and provides a valuable tool for diverse applications across numerous fields. By diligently practicing and understanding the different techniques outlined in this article, you can effectively navigate the world of decimal-to-fraction conversions and confidently apply this knowledge to real-world problems. Remember to always check your work for simplification and accuracy, ensuring you've arrived at the most concise and accurate fractional representation of your decimal value.
Latest Posts
Latest Posts
-
How Many Electrons Can The First Shell Hold
Apr 01, 2025
-
15 6 As A Mixed Number
Apr 01, 2025
-
What Two Monosaccharides Make Up Sucrose
Apr 01, 2025
-
The Heat Of Vaporization Of Water Is 40 66 Kj Mol
Apr 01, 2025
-
Why Are Hydrogen Bonds Important For Life
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is The Fraction For 0.09 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
