What Is Prime Factorization Of 75
listenit
Mar 26, 2025 · 6 min read
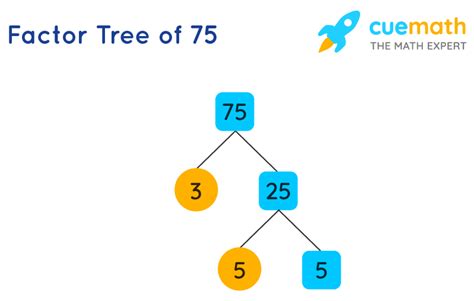
Table of Contents
What is Prime Factorization of 75? A Deep Dive into Number Theory
Prime factorization, a cornerstone of number theory, involves expressing a composite number as a product of its prime factors. Understanding this process is crucial for various mathematical applications, from simplifying fractions to solving complex equations in cryptography. This article delves deep into the prime factorization of 75, explaining the methodology, its significance, and exploring related concepts in number theory.
Understanding Prime Numbers and Composite Numbers
Before embarking on the factorization of 75, let's clarify the fundamental concepts of prime and composite numbers.
Prime Numbers: The Building Blocks
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. Prime numbers are the fundamental building blocks of all other numbers. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. Note that 2 is the only even prime number; all other even numbers are divisible by 2.
Composite Numbers: Products of Primes
A composite number is a positive integer that has at least one divisor other than 1 and itself. In essence, composite numbers can be expressed as a product of prime numbers. For example, 6 is a composite number because it is divisible by 2 and 3 (6 = 2 x 3). Similarly, 12 is a composite number (12 = 2 x 2 x 3). Every composite number can be uniquely expressed as a product of prime numbers, a fact known as the Fundamental Theorem of Arithmetic.
Finding the Prime Factorization of 75: A Step-by-Step Approach
Now, let's apply the concept of prime factorization to the number 75. We need to find the prime numbers that, when multiplied together, equal 75. There are several methods to achieve this:
Method 1: Repeated Division by Prime Numbers
This method involves repeatedly dividing the number by the smallest prime number that divides it evenly, continuing until the quotient is 1.
- Start with the smallest prime number, 2: 75 is not divisible by 2 (it's an odd number).
- Try the next prime number, 3: 75 divided by 3 is 25. So, 75 = 3 x 25.
- Now consider 25: 25 is not divisible by 3, but it is divisible by 5 (25 = 5 x 5).
- Finally, we have: 75 = 3 x 5 x 5. Since 3 and 5 are prime numbers, we have found the prime factorization of 75. We can also write this as 3 x 5².
Method 2: Factor Tree Method
The factor tree method provides a visual representation of the factorization process.
- Start by finding any two factors of 75. A simple choice is 3 and 25.
- Branch out from 75, writing 3 and 25 as its factors.
- Since 3 is a prime number, we circle it.
- 25 is not prime; its factors are 5 and 5.
- Branch out from 25, writing 5 and 5 as its factors.
- Since 5 is a prime number, we circle both 5s.
The prime factors at the end of the branches are 3, 5, and 5. Therefore, the prime factorization of 75 is 3 x 5 x 5 or 3 x 5².
75
/ \
3 25
/ \
5 5
Significance of Prime Factorization
The prime factorization of a number, while seemingly a simple concept, holds immense significance in various mathematical fields:
1. Simplifying Fractions:
Prime factorization is fundamental to simplifying fractions. By expressing the numerator and denominator as products of their prime factors, we can easily identify and cancel common factors, leading to a simplified fraction in its lowest terms.
For example, consider the fraction 75/100. The prime factorization of 75 is 3 x 5², and the prime factorization of 100 is 2² x 5². Therefore, 75/100 = (3 x 5²) / (2² x 5²) = 3/4.
2. Finding the Greatest Common Divisor (GCD) and Least Common Multiple (LCM):
Prime factorization is a powerful tool for finding the greatest common divisor (GCD) and the least common multiple (LCM) of two or more numbers.
-
GCD: The GCD is the largest number that divides all the given numbers without leaving a remainder. To find the GCD using prime factorization, identify the common prime factors with the lowest powers and multiply them together.
-
LCM: The LCM is the smallest number that is a multiple of all the given numbers. To find the LCM using prime factorization, identify all the prime factors with the highest powers and multiply them together.
3. Cryptography:
Prime factorization plays a crucial role in modern cryptography, particularly in the RSA algorithm. RSA relies on the difficulty of factoring very large numbers into their prime factors. The security of many online transactions and secure communications depends on this computationally intensive task.
4. Abstract Algebra:
Prime factorization forms the basis of several concepts in abstract algebra, including unique factorization domains and ideal theory. These are advanced mathematical structures with applications in diverse fields such as algebraic geometry and number theory.
Beyond 75: Exploring Other Factorizations
Let's expand our understanding by examining the prime factorizations of numbers related to 75:
-
Multiples of 75: The prime factorization of multiples of 75 will always include the prime factors of 75 (3 and 5) along with other prime factors depending on the multiplier. For example, the prime factorization of 150 (2 x 75) is 2 x 3 x 5².
-
Factors of 75: The factors of 75 are 1, 3, 5, 15, 25, and 75. The prime factorization of each of these factors will only contain the prime factors 3 and 5 (or neither, in the case of 1).
-
Numbers close to 75: The prime factorization of numbers close to 75 will often be different, highlighting the unique nature of prime factorization for each composite number.
Conclusion: The Importance of Prime Factorization
The prime factorization of 75, 3 x 5², is more than just a simple calculation; it's a gateway to understanding the fundamental structure of numbers and the power of prime numbers. This seemingly basic concept has far-reaching implications in diverse fields, from simplifying fractions to securing online transactions. Mastering prime factorization enhances mathematical proficiency and opens doors to more complex mathematical explorations. By understanding the methods and significance outlined in this article, you can confidently tackle prime factorization problems and appreciate its fundamental role in mathematics. The ability to perform prime factorization efficiently is a valuable skill in various mathematical and computational contexts. Continued practice and exploration of related number theory concepts will further solidify your understanding and problem-solving skills.
Latest Posts
Latest Posts
-
How Many Quarts In Five Gallons
Mar 29, 2025
-
How Do You Make A Supersaturated Solution
Mar 29, 2025
-
Taylor Expansion Of Sqrt 1 X
Mar 29, 2025
-
Calculate The Mass Of The Sun
Mar 29, 2025
-
What Is The Molar Mass Of Na3po4
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about What Is Prime Factorization Of 75 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
