Calculate The Mass Of The Sun
listenit
Mar 29, 2025 · 5 min read
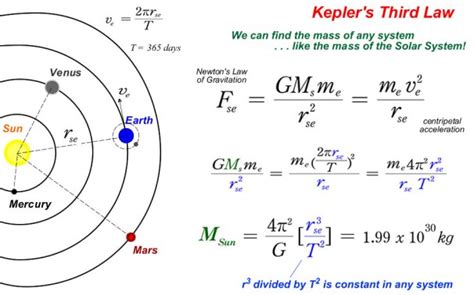
Table of Contents
Calculating the Mass of the Sun: A Deep Dive into Astrophysics
Determining the mass of the Sun, a seemingly daunting task, is actually achievable through a clever application of Newtonian gravity and Kepler's laws of planetary motion. This seemingly simple calculation has profound implications, impacting our understanding of stellar evolution, galactic dynamics, and the very fabric of the universe. This comprehensive guide delves into the intricacies of this calculation, exploring the underlying principles and providing a step-by-step approach.
Understanding the Fundamentals: Gravity and Kepler's Laws
Before we embark on the calculation itself, it's crucial to grasp the foundational concepts:
Newton's Law of Universal Gravitation:
This cornerstone of classical mechanics states that every particle attracts every other particle in the universe with a force proportional to the product of their masses and inversely proportional to the square of the distance between their centers. Mathematically, this is represented as:
F = G * (M * m) / r²
Where:
- F represents the gravitational force
- G is the gravitational constant (approximately 6.674 x 10⁻¹¹ N⋅m²/kg²)
- M and m are the masses of the two objects
- r is the distance between their centers
Kepler's Third Law of Planetary Motion:
This law describes the relationship between the orbital period (T) of a planet and the semi-major axis (a) of its elliptical orbit around the Sun. It states that the square of the orbital period is directly proportional to the cube of the semi-major axis. Expressed mathematically:
T² = (4π²/GM) * a³
This equation is crucial because it directly links the orbital characteristics of a planet to the mass of the Sun (M).
Deriving the Equation for Solar Mass
Combining Newton's Law of Universal Gravitation and Kepler's Third Law allows us to derive an equation for calculating the Sun's mass. Let's consider a planet orbiting the Sun:
-
Centripetal Force: The planet's orbit is maintained by the gravitational force of the Sun acting as a centripetal force. The centripetal force is given by:
F<sub>c</sub> = (m * v²) / r
Where:
- m is the mass of the planet
- v is the orbital velocity of the planet
- r is the distance between the planet and the Sun (approximately the semi-major axis for near-circular orbits)
-
Equating Forces: The gravitational force (F) equals the centripetal force (F<sub>c</sub>):
G * (M * m) / r² = (m * v²) / r
-
Simplifying the Equation: The mass of the planet (m) cancels out, leaving:
G * M / r = v²
-
Relating Velocity and Period: The orbital velocity (v) can be expressed in terms of the orbital period (T) and the circumference of the orbit (approximately 2πr for near-circular orbits):
v = 2πr / T
-
Substituting and Solving for M: Substituting the expression for v into the simplified equation and rearranging to solve for the Sun's mass (M) yields:
M = (4π² * r³) / (G * T²)
Calculating the Mass of the Sun: A Practical Example
To calculate the Sun's mass, we need observational data. Let's use Earth's orbital parameters as an example:
- Earth's orbital period (T): Approximately 365.25 days, or 3.156 x 10⁷ seconds.
- Earth's average distance from the Sun (r): Approximately 149.6 million kilometers, or 1.496 x 10¹¹ meters.
- Gravitational constant (G): 6.674 x 10⁻¹¹ N⋅m²/kg²
Plugging these values into the equation:
M = (4π² * (1.496 x 10¹¹ m)³) / (6.674 x 10⁻¹¹ N⋅m²/kg² * (3.156 x 10⁷ s)²)
This calculation yields a value for the Sun's mass (M) of approximately 1.989 x 10³⁰ kg. This is remarkably close to the currently accepted value of the Sun's mass.
Refinements and Considerations
The calculation above uses simplified assumptions, primarily assuming a perfectly circular orbit. Real planetary orbits are elliptical, requiring the use of the semi-major axis (a) instead of a simple radius (r). Additionally, the influence of other planets on Earth's orbit is neglected in this simplified approach. More sophisticated calculations involve considering these factors and utilizing numerical methods to achieve higher accuracy.
Beyond Earth: Utilizing Other Planets
The same principle can be applied to other planets in our solar system. Using data from planets with different orbital periods and distances, we can obtain multiple independent estimations of the Sun's mass. Averaging these results enhances accuracy and reduces the impact of individual measurement errors. This approach leverages the power of multiple data points to improve the reliability of the calculated solar mass. The more planets used, the better the statistical significance of the result.
Importance of Accurate Solar Mass Determination
Precise determination of the Sun's mass is fundamental to numerous areas of astrophysics:
- Stellar Evolution Models: Accurate solar mass is essential for constructing and validating models of stellar evolution, predicting the lifespan, luminosity, and ultimate fate of stars.
- Galactic Dynamics: Understanding the Sun's mass contributes to our understanding of the dynamics of the Milky Way galaxy, including its gravitational influence on surrounding stars and interstellar matter.
- Exoplanet Research: Determining the masses of exoplanets often relies on observing their gravitational influence on their host stars. Accurate knowledge of the star's mass is crucial for obtaining reliable exoplanet mass estimates.
- Cosmology: The Sun's mass, in conjunction with other astronomical measurements, helps constrain cosmological models, furthering our understanding of the universe's evolution and composition.
Conclusion: A Foundation of Astrophysics
Calculating the mass of the Sun, while seemingly a straightforward application of Newtonian physics, is a cornerstone of astrophysics. The seemingly simple calculation provides essential information for understanding stellar evolution, galactic dynamics, and the larger universe. The precision of this calculation continues to improve as observational data and our understanding of celestial mechanics refine our approaches. This exploration illustrates the power of combining fundamental physics with observational data to unlock profound insights into the cosmos. The journey to accurately determine the Sun's mass is a testament to the enduring power of scientific inquiry and the elegance of the universe's underlying laws.
Latest Posts
Related Post
Thank you for visiting our website which covers about Calculate The Mass Of The Sun . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
