Taylor Expansion Of Sqrt 1 X
listenit
Mar 29, 2025 · 5 min read
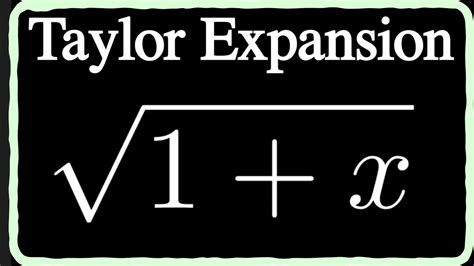
Table of Contents
- Taylor Expansion Of Sqrt 1 X
- Table of Contents
- Taylor Expansion of √(1+x): A Comprehensive Guide
- Understanding Taylor Expansion
- Deriving the Taylor Expansion of √(1+x)
- Connection to the Binomial Theorem
- Radius of Convergence
- Applications of the Taylor Expansion of √(1+x)
- 1. Numerical Approximation:
- 2. Physics and Engineering:
- 3. Finance and Economics:
- 4. Computer Science and Algorithm Design:
- Limitations and Considerations
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
Taylor Expansion of √(1+x): A Comprehensive Guide
The Taylor expansion, a cornerstone of calculus and analysis, provides a powerful method for approximating functions using an infinite sum of terms. This article delves into the Taylor expansion of √(1+x), exploring its derivation, applications, and limitations. We'll also examine its connection to the binomial theorem and discuss its practical use in various fields.
Understanding Taylor Expansion
Before diving into the specifics of √(1+x), let's briefly recap the general concept of a Taylor expansion. For a function f(x) that is infinitely differentiable at a point a, its Taylor expansion around a is given by:
f(x) = f(a) + f'(a)(x-a)/1! + f''(a)(x-a)²/2! + f'''(a)(x-a)³/3! + ...
This infinite series approximates the function f(x) near the point a. The accuracy of the approximation improves as more terms are included. A special case, when a = 0, is called the Maclaurin series.
Deriving the Taylor Expansion of √(1+x)
Let's focus on finding the Taylor expansion of f(x) = √(1+x) around a = 0 (Maclaurin series). This requires calculating successive derivatives of f(x) and evaluating them at x = 0.
- f(x) = (1+x)^(1/2)
- f'(x) = (1/2)(1+x)^(-1/2)
- f''(x) = -(1/4)(1+x)^(-3/2)
- f'''(x) = (3/8)(1+x)^(-5/2)
- f''''(x) = -(15/16)(1+x)^(-7/2)
...and so on. Evaluating these derivatives at x = 0:
- f(0) = 1
- f'(0) = 1/2
- f''(0) = -1/4
- f'''(0) = 3/8
- f''''(0) = -15/16
Substituting these values into the Maclaurin series formula:
√(1+x) ≈ 1 + (1/2)x - (1/8)x² + (1/16)x³ - (5/128)x⁴ + ...
This is the Taylor expansion of √(1+x) around x = 0. Note that this is an approximation; the more terms included, the more accurate the approximation becomes, particularly for values of x close to 0.
Connection to the Binomial Theorem
Interestingly, the Taylor expansion of √(1+x) is closely related to the binomial theorem, which states:
(1+x)^n = 1 + nx + n(n-1)x²/2! + n(n-1)(n-2)x³/3! + ...
for any real number n. In our case, n = 1/2. Substituting this into the binomial theorem yields the same result as our derived Taylor expansion:
(1+x)^(1/2) = 1 + (1/2)x + (1/2)(-1/2)x²/2! + (1/2)(-1/2)(-3/2)x³/3! + ...
This demonstrates the elegant connection between the Taylor expansion and the binomial theorem for fractional exponents.
Radius of Convergence
The Taylor expansion of √(1+x) is only valid within a certain interval, known as the radius of convergence. For this particular series, the radius of convergence is 1. This means the series converges (approaches a finite value) for -1 < x ≤ 1. Outside this interval, the series diverges (approaches infinity). At x = -1, the series converges to 0, while at x = 1, the series converges to √2.
Applications of the Taylor Expansion of √(1+x)
The Taylor expansion of √(1+x) finds applications in various fields, including:
1. Numerical Approximation:
The expansion allows for quick and accurate approximations of square roots for values of x near 0. This is especially useful in scenarios where calculating square roots directly is computationally expensive or impractical. For example, a computer program might use a few terms of the series to efficiently compute approximate square roots.
2. Physics and Engineering:
Many physical phenomena are modeled using equations involving square roots. The Taylor expansion provides a simplified approximation, making calculations and analysis considerably easier, particularly in situations where the variable x is small compared to 1. This is crucial in fields like classical mechanics, where small oscillations are often analyzed.
3. Finance and Economics:
Square roots appear in various financial formulas, such as those calculating standard deviation or option pricing models. The Taylor expansion can be used to create simplified approximations for complex calculations, speeding up computations and improving efficiency in financial modeling.
4. Computer Science and Algorithm Design:
Efficient algorithms often require fast and accurate approximations of mathematical functions. The Taylor expansion of √(1+x) allows for creating efficient routines for square root calculations in software and hardware applications.
Limitations and Considerations
While extremely useful, the Taylor expansion of √(1+x) has limitations:
-
Accuracy: The accuracy of the approximation depends heavily on the number of terms used and the value of x. For larger values of x, more terms are needed to achieve sufficient accuracy, while for values outside the radius of convergence, the approximation becomes unreliable.
-
Computational Cost: Although computationally cheaper than directly calculating the square root for many applications, calculating numerous terms of the expansion can become computationally intensive for very high accuracy requirements.
-
Radius of Convergence: The series only converges within a specific range of x values. For values outside this range, the approximation fails completely.
Conclusion
The Taylor expansion of √(1+x) is a powerful tool for approximating this function, finding widespread applications across diverse fields. Its derivation from the Maclaurin series and its close relationship to the binomial theorem provide a deep understanding of its mathematical basis. While it does have limitations regarding accuracy and the radius of convergence, its efficiency and relative simplicity make it an invaluable technique for approximating square roots in various computational and analytical settings. Understanding these strengths and limitations is critical for its effective and responsible use in practical applications. This detailed exploration provides a comprehensive understanding of this essential tool in mathematics and beyond. Remember that while this expansion provides a valuable approximation, for high precision, the use of dedicated numerical methods remains necessary.
Latest Posts
Latest Posts
-
How Much Feet Is 100 Yards
Apr 02, 2025
-
How Many 1 3 Are In 1 2
Apr 02, 2025
-
What Is 20 Percent Of 80
Apr 02, 2025
-
Is Water Evaporating A Physical Change
Apr 02, 2025
-
Atoms That Have Gained Or Lost Electrons
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Taylor Expansion Of Sqrt 1 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
