What Is Lcm Of 8 And 12
listenit
Mar 28, 2025 · 5 min read
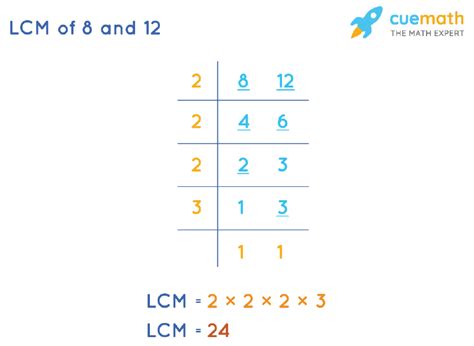
Table of Contents
What is the LCM of 8 and 12? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly crucial in areas like fractions, algebra, and even music theory. This article will explore the LCM of 8 and 12, providing multiple methods for calculation and demonstrating its practical applications. We'll delve beyond the simple answer to equip you with a comprehensive understanding of this important mathematical concept.
Understanding Least Common Multiples (LCM)
Before we tackle the LCM of 8 and 12, let's establish a solid foundation. The least common multiple of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that can be divided evenly by all the given numbers without leaving a remainder.
Key Concepts:
- Multiple: A multiple of a number is the result of multiplying that number by any integer (whole number). For example, multiples of 8 are 8, 16, 24, 32, and so on.
- Common Multiple: A common multiple of two or more numbers is a number that is a multiple of all of them. For example, common multiples of 8 and 12 include 24, 48, 72, etc.
- Least Common Multiple (LCM): The smallest of these common multiples is the least common multiple.
Methods for Finding the LCM of 8 and 12
There are several effective ways to calculate the LCM of 8 and 12. Let's explore the most common approaches:
1. Listing Multiples Method
This is a straightforward method, especially useful for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56...
- Multiples of 12: 12, 24, 36, 48, 60...
By comparing the lists, we see that the smallest common multiple is 24. Therefore, the LCM of 8 and 12 is 24.
2. Prime Factorization Method
This method is more efficient for larger numbers and provides a deeper understanding of the LCM's structure. It involves finding the prime factors of each number.
- Prime factorization of 8: 2 x 2 x 2 = 2³
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
To find the LCM, we take the highest power of each prime factor present in either factorization:
- Highest power of 2: 2³ = 8
- Highest power of 3: 3¹ = 3
Multiply these highest powers together: 8 x 3 = 24. Therefore, the LCM of 8 and 12 is 24.
3. Greatest Common Divisor (GCD) Method
This method uses the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The GCD is the largest number that divides both numbers without leaving a remainder.
- Finding the GCD of 8 and 12:
- Factors of 8: 1, 2, 4, 8
- Factors of 12: 1, 2, 3, 4, 6, 12
- The greatest common factor is 4. Therefore, GCD(8, 12) = 4.
The relationship between LCM and GCD is given by the formula:
LCM(a, b) = (|a x b|) / GCD(a, b)
Substituting the values for 8 and 12:
LCM(8, 12) = (|8 x 12|) / 4 = 96 / 4 = 24
This confirms that the LCM of 8 and 12 is 24.
Applications of LCM
The concept of LCM has numerous practical applications across various fields:
1. Fraction Addition and Subtraction
Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators. For example, to add 1/8 and 1/12, we need to find the LCM of 8 and 12, which is 24. We then rewrite the fractions with a denominator of 24 before adding them:
(3/24) + (2/24) = 5/24
2. Scheduling and Cyclical Events
LCM is useful in solving problems related to repeating events or schedules. For example, if one event occurs every 8 days and another every 12 days, the LCM (24) tells us when both events will occur on the same day again.
3. Music Theory
In music, the LCM helps determine the least common denominator for rhythmic patterns and note durations. It ensures that different rhythmic patterns align correctly, creating harmonious and predictable musical structures.
4. Gear Ratios and Mechanical Systems
In mechanical engineering, LCM is used in calculating gear ratios and synchronizing the speeds of rotating components in machines. Understanding LCM helps optimize the performance and efficiency of mechanical systems.
5. Project Management
In project scheduling and management, LCM can help determine the optimal timing for tasks that need to be completed simultaneously or sequentially, ensuring efficient resource allocation and project completion.
Beyond the Basics: Extending LCM Concepts
While we've focused on finding the LCM of two numbers, the concept extends to finding the LCM of three or more numbers. The methods discussed—prime factorization and the GCD method—can be adapted to handle multiple numbers. For example, to find the LCM of 8, 12, and 15:
-
Prime Factorization:
- 8 = 2³
- 12 = 2² x 3
- 15 = 3 x 5
-
Finding the LCM: Take the highest power of each prime factor: 2³ x 3 x 5 = 8 x 3 x 5 = 120. The LCM of 8, 12, and 15 is 120.
Conclusion: Mastering LCM for Mathematical Success
Understanding the LCM is essential for a strong foundation in mathematics. Whether you're tackling fractions, solving scheduling problems, or exploring more advanced mathematical concepts, mastering the LCM provides a powerful tool for problem-solving and a deeper understanding of numerical relationships. The various methods presented here offer flexibility depending on the complexity of the problem, ensuring that you have the right approach for any situation. By understanding both the calculation methods and the wide range of applications, you'll be well-equipped to confidently tackle LCM problems and appreciate its significance in diverse fields. Remember, practice is key – the more you work with LCM problems, the more intuitive and effortless the process will become.
Latest Posts
Latest Posts
-
Is Gasoline Evaporating A Chemical Change
Mar 31, 2025
-
What Is Half Of A Mile In Feet
Mar 31, 2025
-
Common Factors Of 20 And 36
Mar 31, 2025
-
Simplify The Square Root Of 288
Mar 31, 2025
-
How Many Protons Are In Carbon 14
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is Lcm Of 8 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
