Simplify The Square Root Of 288
listenit
Mar 31, 2025 · 4 min read
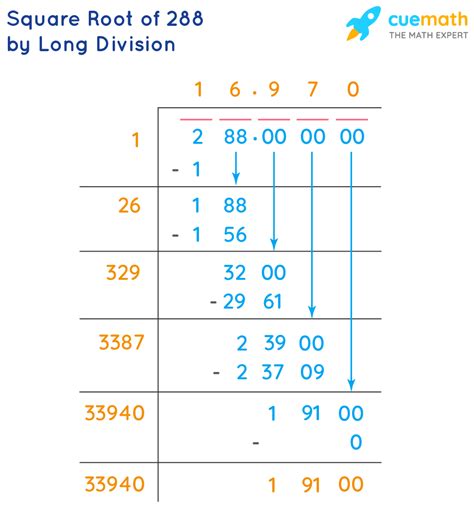
Table of Contents
Simplifying the Square Root of 288: A Comprehensive Guide
Simplifying radicals, such as the square root of 288 (√288), might seem daunting at first. However, with a systematic approach and understanding of fundamental mathematical principles, this process becomes straightforward and even enjoyable. This comprehensive guide will break down the simplification of √288 step-by-step, offering multiple methods and explaining the underlying concepts. We'll also explore broader applications and related concepts to solidify your understanding of radical simplification.
Understanding Square Roots and Radicals
Before diving into simplifying √288, let's refresh our understanding of square roots and radicals. A square root is a number that, when multiplied by itself, equals a given number. For example, the square root of 9 (√9) is 3 because 3 * 3 = 9. Radicals are expressions containing roots, such as square roots (√), cube roots (∛), and higher-order roots.
The process of simplifying radicals involves finding the simplest equivalent expression for a radical. This often means removing perfect squares (or perfect cubes, etc.) from under the radical sign.
Method 1: Prime Factorization
The most common and reliable method for simplifying square roots involves prime factorization. This method breaks down a number into its prime factors – numbers divisible only by 1 and themselves.
Steps:
-
Find the prime factorization of 288:
We can start by dividing 288 by the smallest prime number, 2:
288 ÷ 2 = 144 144 ÷ 2 = 72 72 ÷ 2 = 36 36 ÷ 2 = 18 18 ÷ 2 = 9 9 ÷ 3 = 3 3 ÷ 3 = 1
Therefore, the prime factorization of 288 is 2 x 2 x 2 x 2 x 2 x 3 x 3 = 2<sup>5</sup> x 3<sup>2</sup>
-
Identify perfect squares:
Look for pairs of identical prime factors. In our factorization, we have five 2s and two 3s. We can identify a pair of 2s, another pair of 2s, and a pair of 3s. Each pair represents a perfect square.
-
Simplify the radical:
Rewrite the expression using the identified perfect squares:
√288 = √(2<sup>2</sup> x 2<sup>2</sup> x 2 x 3<sup>2</sup>)
Since √(a²)= a, we can simplify:
√288 = 2 x 2 x 3 x √2 = 12√2
Therefore, the simplified form of √288 is 12√2.
Method 2: Identifying Perfect Square Factors
This method is a shortcut to prime factorization. It involves finding the largest perfect square that divides evenly into 288.
Steps:
-
Identify perfect square factors:
Consider perfect squares: 4, 9, 16, 25, 36, 64, 144, etc.
-
Find the largest perfect square factor:
We can see that 144 is the largest perfect square that divides evenly into 288 (288 ÷ 144 = 2).
-
Simplify the radical:
Rewrite the expression using the perfect square factor:
√288 = √(144 x 2) = √144 x √2 = 12√2
Again, the simplified form of √288 is 12√2.
Method 3: Using a Calculator (with caveats)
While calculators can provide the decimal approximation of √288 (approximately 16.97), they don't directly give the simplified radical form. Calculators are helpful for checking your work, but they don't show the underlying mathematical process which is crucial for understanding. You need to rely on the prime factorization or perfect square factor methods to arrive at the simplified radical form.
Applications of Radical Simplification
Simplifying radicals is fundamental in various mathematical fields, including:
- Algebra: Solving quadratic equations often results in solutions containing radicals, which need simplification for accurate interpretation.
- Geometry: Calculating distances, areas, and volumes of geometric shapes frequently involves radicals. Simplifying these radicals makes calculations cleaner and easier to understand.
- Trigonometry: Trigonometric functions and identities often involve radicals, requiring simplification for precise calculations and problem-solving.
- Calculus: Derivatives and integrals can produce expressions involving radicals, which need simplification for analysis and interpretation.
Understanding Irrational Numbers
The simplified form of √288, 12√2, highlights an important concept: irrational numbers. √2 is an irrational number, meaning it cannot be expressed as a simple fraction. Its decimal representation goes on forever without repeating. Simplifying radicals often leaves us with irrational numbers, represented by the radical symbol.
Further Practice and Challenges
To strengthen your understanding, try simplifying other square roots using the methods described above:
- √72
- √108
- √500
- √1250
These exercises will reinforce your skills in identifying prime factors and perfect squares, leading to proficient simplification of radicals.
Conclusion: Mastering Radical Simplification
Simplifying radicals, such as √288, is a fundamental skill in mathematics. Mastering this skill through understanding prime factorization and identifying perfect squares allows for efficient and accurate manipulation of radical expressions across various mathematical disciplines. While calculators offer numerical approximations, understanding the underlying mathematical process is crucial for deeper comprehension and problem-solving. Remember to always strive for the simplest radical form, as this provides the most accurate and interpretable representation of the value. By practicing the techniques outlined above, you'll build confidence and proficiency in simplifying any square root you encounter.
Latest Posts
Latest Posts
-
What Is The Proper Name For Mgf2
Apr 02, 2025
-
Unit Of Measurement For Kinetic Energy
Apr 02, 2025
-
How Do Lichens Contribute To Primary Succession
Apr 02, 2025
-
Number Of Valence Electrons In Calcium
Apr 02, 2025
-
How Many Valence Electrons In Calcium
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Simplify The Square Root Of 288 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
