Unit Of Measurement For Kinetic Energy
listenit
Apr 02, 2025 · 5 min read
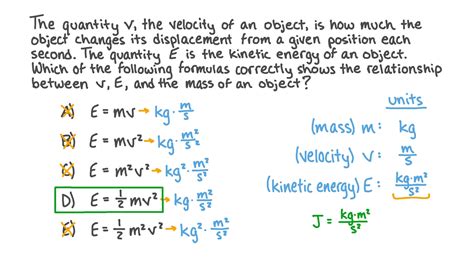
Table of Contents
Unit of Measurement for Kinetic Energy: A Comprehensive Guide
Kinetic energy, the energy possessed by an object due to its motion, is a fundamental concept in physics with far-reaching applications across various fields. Understanding its measurement is crucial for accurately describing and predicting the behavior of moving objects, from microscopic particles to macroscopic systems. This comprehensive guide delves into the units used to quantify kinetic energy, exploring their derivations, interconversions, and practical applications.
The Fundamental Formula: Defining Kinetic Energy
Before diving into units, it's essential to establish the fundamental formula for kinetic energy:
KE = ½mv²
Where:
- KE represents kinetic energy.
- m represents the mass of the object.
- v represents the velocity of the object.
This simple yet powerful equation reveals the direct relationship between kinetic energy, mass, and velocity. A doubling of mass or a doubling of velocity results in a quadrupling of kinetic energy. This fundamental relationship underpins the choice of units used to measure kinetic energy.
The SI Unit: Joule (J)
The standard unit of measurement for kinetic energy within the International System of Units (SI) is the Joule (J). The Joule is a derived unit, meaning it's defined in terms of other fundamental SI units. From the kinetic energy formula, we can derive the Joule's composition:
- Mass (m): Measured in kilograms (kg)
- Velocity (v): Measured in meters per second (m/s)
Therefore, the Joule can be expressed as:
1 J = 1 kg⋅m²/s²
This signifies that one Joule of kinetic energy is equivalent to the energy required to accelerate a one-kilogram mass at a rate of one meter per second squared over a distance of one meter. The Joule is a versatile unit applicable across diverse kinetic energy scenarios, from the movement of subatomic particles to the motion of large-scale machinery.
Practical Applications of the Joule:
- Mechanical Systems: Analyzing the energy transfer in machines, engines, and other mechanical devices. Calculating work done by forces, potential energy conversions, and impact forces.
- Molecular and Atomic Physics: Describing the kinetic energy of molecules and atoms in gases, liquids, and solids, which directly relates to temperature. This plays a crucial role in understanding thermodynamics and statistical mechanics.
- Nuclear Physics: Studying the kinetic energy of particles in nuclear reactions, such as alpha decay and fission. This aids in understanding nuclear stability, radioactive decay, and energy generation in nuclear reactors.
- Electronics: Characterizing the energy of moving electrons in circuits and electronic devices. This is crucial for circuit design, power consumption analysis, and understanding signal transmission.
Other Units of Measurement for Kinetic Energy
While the Joule is the preferred and universally accepted SI unit, other units may be used depending on the context and scale of the problem. These often arise from the use of different unit systems or when dealing with extremely large or small values of kinetic energy.
1. Erg (erg): CGS Unit
In the centimeter-gram-second (CGS) system of units, the unit of kinetic energy is the erg. One erg is defined as:
1 erg = 1 g⋅cm²/s²
The erg is significantly smaller than the Joule. The conversion factor is:
1 J = 10⁷ erg
Ergs are less commonly used in modern physics and engineering but remain relevant in some specialized areas of research.
2. Electronvolt (eV): Atomic and Subatomic Physics
In atomic and subatomic physics, the electronvolt (eV) is frequently used. It represents the energy gained by a single electron when accelerated across a potential difference of one volt.
1 eV ≈ 1.602 × 10⁻¹⁹ J
Electronvolts are particularly convenient when dealing with the kinetic energies of electrons, protons, and other charged particles in atomic and nuclear processes. Larger multiples like kiloelectronvolts (keV), megaelectronvolts (MeV), and gigaelectronvolts (GeV) are often employed for higher energy phenomena.
3. BTU (British Thermal Unit): Thermodynamics and Engineering
The British Thermal Unit (BTU) is an energy unit commonly used in thermodynamics and engineering, particularly in the United States. One BTU is defined as the amount of energy needed to raise the temperature of one pound of water by one degree Fahrenheit. While not directly derived from the kinetic energy formula, the BTU can be used to express kinetic energy, especially when dealing with thermal processes and energy conversions.
1 BTU ≈ 1055 J
Unit Conversions and Dimensional Analysis
Accurate conversion between different units of kinetic energy is essential for consistent calculations and accurate analysis. Dimensional analysis plays a critical role in ensuring the correctness of unit conversions. This involves checking that the dimensions (mass, length, time) are consistent on both sides of the equation.
Here are some common conversions:
- Joules to Ergs: Multiply the value in Joules by 10⁷ to obtain the equivalent value in ergs.
- Joules to Electronvolts: Divide the value in Joules by 1.602 × 10⁻¹⁹ to obtain the equivalent value in electronvolts.
- Joules to BTUs: Divide the value in Joules by 1055 to obtain the equivalent value in BTUs.
Practical Examples: Calculating Kinetic Energy in Different Units
Let's illustrate the application of different kinetic energy units with a few examples:
Example 1: A rolling ball
A ball with a mass of 0.5 kg rolls at a velocity of 2 m/s. Calculate its kinetic energy in Joules:
KE = ½ * 0.5 kg * (2 m/s)² = 1 J
Example 2: An electron in an electric field
An electron is accelerated through a potential difference of 100 V. Calculate its kinetic energy in electronvolts:
KE = 100 eV (Since 1 eV is the energy gained by an electron across 1V)
To convert this to Joules:
KE = 100 eV * 1.602 × 10⁻¹⁹ J/eV ≈ 1.602 × 10⁻¹⁷ J
Example 3: A moving vehicle
A car with a mass of 1000 kg travels at a speed of 20 m/s. Calculate its kinetic energy in Joules and then convert it to BTUs:
KE = ½ * 1000 kg * (20 m/s)² = 200,000 J
To convert to BTUs:
KE = 200,000 J / 1055 J/BTU ≈ 189.5 BTUs
Conclusion
The unit of measurement for kinetic energy, primarily the Joule, is a cornerstone of physics and engineering. Understanding its derivation, the relationship to other units, and practical applications are essential for accurate analysis across diverse scientific and technological domains. The flexibility of using different units depending on the context underscores the importance of mastering unit conversions and maintaining dimensional consistency in all calculations. By understanding the nuances of these units and their conversions, one can effectively describe and manipulate the energy of motion in various systems, from the smallest particles to the largest machines. This knowledge forms a critical foundation for further exploration into more complex energy concepts and their applications.
Latest Posts
Latest Posts
-
Dissolution Of Sodium Chloride In Water
Apr 03, 2025
-
Which State Of Matter Takes The Shape Of Its Container
Apr 03, 2025
-
Whats The Square Root Of 145
Apr 03, 2025
-
What Is The Highest Common Factor Of 24 And 32
Apr 03, 2025
-
X 3y 9 In Slope Intercept Form
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Unit Of Measurement For Kinetic Energy . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
