Whats The Square Root Of 145
listenit
Apr 03, 2025 · 4 min read
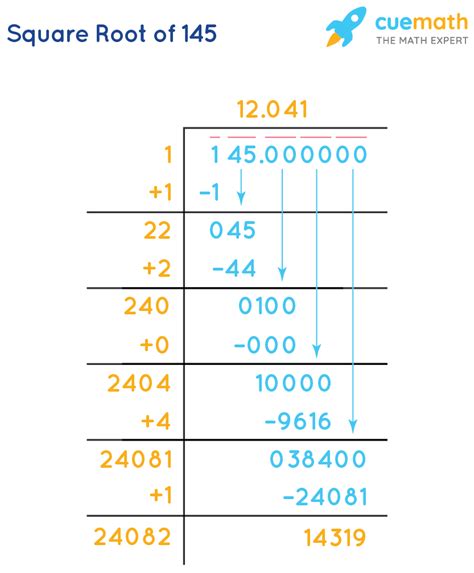
Table of Contents
What's the Square Root of 145? A Deep Dive into Square Roots and Approximation Techniques
The question, "What's the square root of 145?" seems simple enough. However, delving into the answer reveals a fascinating journey into the world of mathematics, exploring different methods of calculation, the nature of irrational numbers, and the practical applications of square roots. This article will not only provide the answer but also equip you with a comprehensive understanding of how to approach similar problems.
Understanding Square Roots
Before we tackle the square root of 145 specifically, let's establish a fundamental understanding of what a square root represents. The square root of a number (x) is a value (y) that, when multiplied by itself, equals x. In mathematical notation: y² = x. Therefore, y = √x. This 'y' is the square root.
For example:
- The square root of 9 (√9) is 3, because 3 * 3 = 9.
- The square root of 16 (√16) is 4, because 4 * 4 = 16.
But what about numbers that don't have perfect square roots, like 145? These numbers result in irrational numbers, meaning their decimal representation goes on forever without repeating.
Calculating the Square Root of 145
145 isn't a perfect square, meaning its square root is an irrational number. We can't find an exact answer; instead, we need to approximate it. Here are several methods:
1. Using a Calculator: The Simplest Approach
The easiest way to find the approximate square root of 145 is to use a calculator. Most calculators have a square root function (√). Simply input 145 and press the √ button. You'll get a result close to 12.0415945788. This is an approximation, as the actual value extends infinitely.
2. The Babylonian Method (or Heron's Method): An Iterative Approach
The Babylonian method is an ancient algorithm for approximating square roots. It's an iterative process, meaning you repeat the steps until you reach the desired level of accuracy. Here's how it works:
-
Make an initial guess: Start with a guess for the square root of 145. Let's guess 12.
-
Improve the guess: Divide 145 by your guess (145 / 12 ≈ 12.0833).
-
Average the results: Average the result from step 2 and your initial guess: (12 + 12.0833) / 2 ≈ 12.0416.
-
Repeat: Use the result from step 3 as your new guess and repeat steps 2 and 3. The more you iterate, the closer you get to the actual square root.
Let's do one more iteration:
- 145 / 12.0416 ≈ 12.0415
- (12.0416 + 12.0415) / 2 ≈ 12.04155
As you can see, the approximation is converging towards the value obtained from a calculator.
3. Prime Factorization and Simplification: Understanding the Number's Structure
While we cannot find a perfect square root, we can simplify the expression using prime factorization. 145 can be factored as 5 x 29. Since neither 5 nor 29 are perfect squares, we cannot simplify the square root further. Therefore, √145 remains as it is, representing an irrational number.
4. Using Logarithms: A Less Common but Powerful Method
Logarithms offer another way to approximate square roots. The formula is:
√x = 10^(log₁₀(x)/2)
Applying this to 145:
√145 = 10^(log₁₀(145)/2) ≈ 12.04
This method requires a logarithm table or a calculator with logarithmic functions.
Practical Applications of Square Roots
Square roots aren't just abstract mathematical concepts; they have numerous practical applications in various fields:
-
Physics: Calculating speed, velocity, and acceleration often involves square roots. For example, calculating the distance an object falls due to gravity uses a square root in the formula.
-
Engineering: Structural design, calculating distances and dimensions, and determining forces frequently involve square root calculations.
-
Computer Graphics: Rendering and transformations in 2D and 3D graphics use square roots extensively for distance calculations and vector operations.
-
Finance: Calculating compound interest, standard deviation in investments, and other financial models use square roots.
-
Geometry: Finding the length of a diagonal in a rectangle or the distance between two points uses the Pythagorean theorem, which inherently involves square roots.
Beyond the Square Root of 145: Exploring Related Concepts
Understanding the square root of 145 opens doors to exploring other mathematical concepts:
-
Higher-Order Roots: Just as we have square roots (second roots), we also have cube roots (third roots), fourth roots, and so on. These represent values that, when multiplied by themselves a certain number of times, equal the original number.
-
Complex Numbers: When dealing with the square roots of negative numbers, we enter the realm of complex numbers, which involve the imaginary unit 'i' (where i² = -1).
-
Approximation Techniques: The methods discussed (Babylonian method, logarithms) are examples of numerical analysis techniques used to solve problems that don't have exact analytical solutions.
Conclusion: Mastering Square Roots and Beyond
While the simple question, "What's the square root of 145?" might seem straightforward, its answer unveils a deeper appreciation for the intricacies of mathematics. We've explored multiple methods for calculating this irrational number, understood its practical significance, and touched upon related mathematical concepts. Whether you're a student, an engineer, or simply curious about numbers, mastering the concept of square roots empowers you to tackle more complex problems and appreciate the beauty and power of mathematics. Remember, the journey of understanding is often more rewarding than the destination itself. So keep exploring, keep questioning, and keep learning!
Latest Posts
Latest Posts
-
Where Does Replication Occur In Eukaryotic Cells
Apr 03, 2025
-
What Is 33 Percent Of 60
Apr 03, 2025
-
How To Find The Measure Of One Interior Angle
Apr 03, 2025
-
What Is The Percentage Of 0 25
Apr 03, 2025
-
How To Find The Slope Of Demand Curve
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Whats The Square Root Of 145 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
