What Is Greater 3/4 Or 2/3
listenit
Mar 26, 2025 · 6 min read
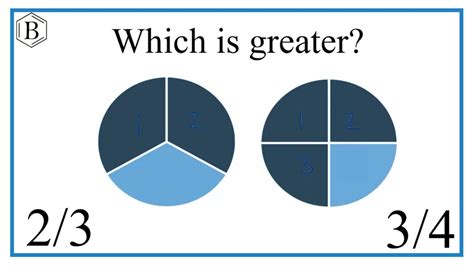
Table of Contents
What's Greater: 3/4 or 2/3? A Deep Dive into Fraction Comparison
Determining which fraction is greater, 3/4 or 2/3, might seem like a simple task, especially for those well-versed in mathematics. However, understanding the underlying principles and different methods for comparing fractions is crucial for building a strong foundation in arithmetic and problem-solving. This comprehensive guide explores various techniques to compare these two fractions, delving deeper into the concepts of fractions, equivalent fractions, and common denominators. We will also discuss the practical applications of this knowledge and how it relates to other mathematical concepts.
Understanding Fractions: A Refresher
Before diving into the comparison, let's revisit the fundamentals of fractions. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number representing the number of parts you have.
- Denominator: The bottom number indicating the total number of equal parts the whole is divided into.
In our case, we have 3/4 and 2/3. 3/4 means we have 3 out of 4 equal parts, while 2/3 means we have 2 out of 3 equal parts. The key to comparing them lies in finding a common ground for comparison.
Method 1: Finding a Common Denominator
This is arguably the most common and straightforward method for comparing fractions. The idea is to convert both fractions into equivalent fractions with the same denominator. The least common denominator (LCD) is the smallest multiple that both denominators share.
1. Finding the LCD:
For 4 and 3, the multiples are:
- Multiples of 4: 4, 8, 12, 16, 20...
- Multiples of 3: 3, 6, 9, 12, 15...
The least common multiple (LCM) of 4 and 3 is 12. Therefore, our LCD is 12.
2. Converting to Equivalent Fractions:
To convert 3/4 to an equivalent fraction with a denominator of 12, we multiply both the numerator and the denominator by 3:
(3 x 3) / (4 x 3) = 9/12
Similarly, to convert 2/3 to an equivalent fraction with a denominator of 12, we multiply both the numerator and the denominator by 4:
(2 x 4) / (3 x 4) = 8/12
3. Comparison:
Now we can easily compare 9/12 and 8/12. Since 9 > 8, we conclude that 9/12 > 8/12, therefore 3/4 > 2/3.
Method 2: Converting to Decimals
Another effective method involves converting both fractions into their decimal equivalents. This approach can be particularly useful when dealing with more complex fractions or when a decimal representation is needed for further calculations.
1. Decimal Conversion:
To convert 3/4 to a decimal, we divide the numerator (3) by the denominator (4):
3 ÷ 4 = 0.75
Similarly, for 2/3:
2 ÷ 3 ≈ 0.6667 (this is a repeating decimal)
2. Comparison:
Now we compare the decimal values: 0.75 and 0.6667. Clearly, 0.75 > 0.6667, confirming that 3/4 > 2/3.
Method 3: Visual Representation (Using Models)
For a more intuitive understanding, especially for beginners, visualizing fractions using models like circles or bars can be highly beneficial.
Imagine two circles. Divide the first circle into four equal parts and shade three of them (representing 3/4). Divide the second circle into three equal parts and shade two of them (representing 2/3). Visually comparing the shaded areas clearly shows that the shaded area in the first circle (3/4) is larger than the shaded area in the second circle (2/3).
Method 4: Cross-Multiplication
This method provides a quick and efficient way to compare two fractions without finding a common denominator. It involves multiplying the numerator of one fraction by the denominator of the other and vice versa.
1. Cross-Multiplication:
Multiply the numerator of 3/4 (which is 3) by the denominator of 2/3 (which is 3): 3 x 3 = 9
Multiply the numerator of 2/3 (which is 2) by the denominator of 3/4 (which is 4): 2 x 4 = 8
2. Comparison:
Compare the products: 9 and 8. Since 9 > 8, we conclude that 3/4 > 2/3.
Practical Applications and Real-World Examples
The ability to compare fractions is not just an abstract mathematical exercise; it has numerous practical applications in daily life and various professions. Here are a few examples:
-
Baking and Cooking: Recipes often require precise measurements of ingredients, and understanding fractions is crucial for accurately following instructions and achieving desired results. For example, you need to determine whether you have enough 3/4 cup of flour or 2/3 cup required for a recipe.
-
Construction and Engineering: Precise measurements are critical in construction and engineering projects. Calculating the correct proportions of materials, determining angles, and ensuring structural integrity often involve working with fractions. Imagine comparing the thickness of two metal sheets – one 3/4 inch thick and the other 2/3 inch.
-
Finance and Budgeting: Managing personal finances, understanding loan interest rates, and calculating discounts often involve fraction computations. For instance, you might compare two interest rates: 3/4% and 2/3%.
-
Data Analysis and Statistics: Data analysis involves representing data using fractions and percentages, often requiring comparing different fractions to draw conclusions. For example, a survey may show that 3/4 of respondents prefer option A while 2/3 prefer option B, highlighting which is more preferred.
-
Time Management: Understanding and working with fractions of time (e.g., 3/4 of an hour or 2/3 of a day) is important for efficient time management and scheduling.
Beyond the Basics: Extending the Concepts
Understanding fraction comparison forms the foundation for more advanced mathematical concepts. These include:
-
Improper Fractions and Mixed Numbers: This involves working with fractions where the numerator is larger than the denominator (improper fractions) and converting them to mixed numbers (a combination of a whole number and a fraction).
-
Fraction Operations: The ability to compare fractions is crucial for performing operations such as addition, subtraction, multiplication, and division of fractions.
-
Ratio and Proportion: Ratios and proportions involve comparing two quantities, often expressed as fractions. Solving proportion problems requires a solid understanding of fraction manipulation and comparison.
-
Percentage Calculations: Percentages are closely related to fractions. Converting fractions to percentages and vice versa often involves comparing fractional values.
Conclusion: Mastering Fraction Comparison
Comparing fractions, while seemingly elementary, is a fundamental skill that underpins many mathematical operations and real-world applications. The methods discussed in this article – finding a common denominator, converting to decimals, visual representation, and cross-multiplication – provide various approaches to tackle this task. Mastering these methods equips individuals with a robust mathematical foundation, enhances problem-solving abilities, and opens doors to understanding more advanced mathematical concepts. Remember, practice is key to developing fluency and confidence in comparing fractions. By consistently engaging with fraction comparison problems, you will solidify your understanding and improve your overall mathematical proficiency.
Latest Posts
Latest Posts
-
What Percentage Is 38 Out Of 40
Mar 29, 2025
-
What Does The Prefix Hydro Mean
Mar 29, 2025
-
How Do You Find The Equation Of A Secant Line
Mar 29, 2025
-
How Do You Factor 3x 2 5x 2
Mar 29, 2025
-
Whats The Atomic Number For Helium
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about What Is Greater 3/4 Or 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
