What Is A Factor Of 57
listenit
Apr 04, 2025 · 5 min read
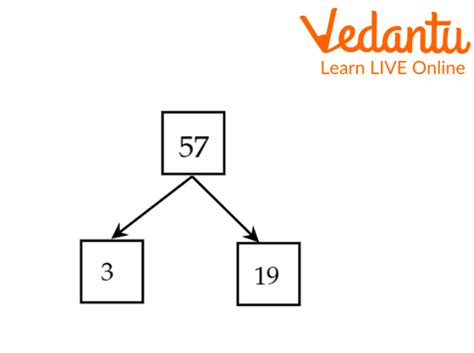
Table of Contents
What is a Factor of 57? A Deep Dive into Number Theory
Finding the factors of a number might seem like a simple arithmetic exercise, but it delves into the fascinating world of number theory, with implications in various fields like cryptography and computer science. This article explores the concept of factors, specifically focusing on the factors of 57, providing a comprehensive understanding of the process and its underlying mathematical principles. We'll move beyond simply listing the factors to explore related concepts and applications.
Understanding Factors
Before we dive into the factors of 57, let's establish a solid foundation. A factor (also known as a divisor) of a number is a whole number that divides the number exactly without leaving a remainder. In simpler terms, if you can divide a number by another number and get a whole number as the result, the number you divided by is a factor.
For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. This is because 12 is divisible by each of these numbers without leaving a remainder.
Prime Factorization: The Building Blocks of Numbers
Prime factorization is a crucial concept in understanding factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Examples include 2, 3, 5, 7, 11, and so on. Prime factorization is the process of expressing a number as a product of its prime factors. This representation is unique for every number (excluding the order of factors).
Prime factorization is a powerful tool because it helps us find all the factors of a number systematically.
Finding the Factors of 57
Now, let's tackle the main question: what are the factors of 57? We can approach this in several ways:
Method 1: Trial and Error
We can start by systematically testing whole numbers to see if they divide 57 without leaving a remainder. We begin with 1, then 2, 3, and so on.
- 57 ÷ 1 = 57
- 57 ÷ 3 = 19
- 57 ÷ 19 = 3
- 57 ÷ 57 = 1
We find that 1, 3, 19, and 57 are the factors of 57.
Method 2: Prime Factorization
Let's find the prime factorization of 57. We start by dividing 57 by the smallest prime number, 2. Since 57 is odd, it's not divisible by 2. The next prime number is 3.
57 ÷ 3 = 19
19 is also a prime number. Therefore, the prime factorization of 57 is 3 x 19.
Knowing the prime factorization is invaluable. From this, we can easily list all the factors:
- 1 (always a factor of any number)
- 3 (one of the prime factors)
- 19 (the other prime factor)
- 57 (the number itself)
Why Understanding Factors is Important
Understanding factors isn't just an academic exercise; it has practical applications in various areas:
1. Simplifying Fractions
Factors are essential for simplifying fractions. To reduce a fraction to its simplest form, we find the greatest common factor (GCF) of the numerator and the denominator and divide both by the GCF.
For instance, if we have the fraction 57/114, we find that the GCF of 57 and 114 is 57. Dividing both the numerator and denominator by 57, we get the simplified fraction 1/2.
2. Solving Equations
Factors are frequently used in solving algebraic equations, particularly quadratic equations. Factoring a quadratic expression helps to find its roots (the values of the variable that make the expression equal to zero).
3. Cryptography
Prime factorization plays a vital role in modern cryptography, especially in RSA encryption. RSA relies on the difficulty of factoring large numbers into their prime components. The security of many online transactions depends on this principle.
4. Computer Science
Factors are crucial in various algorithms and data structures in computer science. For example, understanding prime factorization is important in certain hashing algorithms and in optimizing code for efficiency.
Exploring Related Concepts
Let's delve into some related number theory concepts:
1. Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest number that divides two or more numbers without leaving a remainder. Finding the GCF is useful in simplifying fractions and solving various mathematical problems. For instance, the GCF of 57 and 85 is 19.
2. Least Common Multiple (LCM)
The least common multiple (LCM) is the smallest positive number that is a multiple of two or more numbers. LCM is useful in solving problems involving fractions, cycles, and other mathematical situations where finding the smallest common multiple is necessary.
3. Divisibility Rules
Divisibility rules are shortcuts to determine if a number is divisible by another number without performing actual division. For example, a number is divisible by 3 if the sum of its digits is divisible by 3. Understanding divisibility rules can significantly speed up the process of finding factors.
Advanced Concepts and Applications
The concept of factors extends into more advanced mathematical topics:
-
Modular Arithmetic: This branch of number theory deals with remainders after division. Factors play a key role in understanding modular arithmetic, particularly in cryptography.
-
Abstract Algebra: Factors and divisors are fundamental concepts in abstract algebra, where they are generalized to more abstract structures like rings and ideals.
-
Number Theory Research: Active research in number theory continues to explore the properties of factors, prime numbers, and their distribution. These explorations have deep implications for our understanding of mathematics and its applications.
Conclusion: The Significance of Factors
The seemingly simple question, "What is a factor of 57?" opens the door to a rich world of mathematical concepts and applications. From basic arithmetic to advanced cryptography, the understanding of factors is essential. By exploring prime factorization, greatest common factors, and related concepts, we gain a deeper appreciation for the underlying structure of numbers and their significance in various fields. The seemingly simple task of finding the factors of 57 serves as a stepping stone to a much broader and fascinating area of mathematical inquiry. The exploration continues, and the more we delve into the world of numbers, the more we uncover their intricate beauty and utility.
Latest Posts
Latest Posts
-
Anti Derivative Of Square Root Of X
Apr 05, 2025
-
Greatest Common Factor Of 24 And 36
Apr 05, 2025
-
What Is 3 4 5 As A Decimal
Apr 05, 2025
-
What Is The Range Of The Data Below
Apr 05, 2025
-
What Is The Electron Configuration Of Ga
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about What Is A Factor Of 57 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
