What Is The Range Of The Data Below
listenit
Apr 05, 2025 · 5 min read
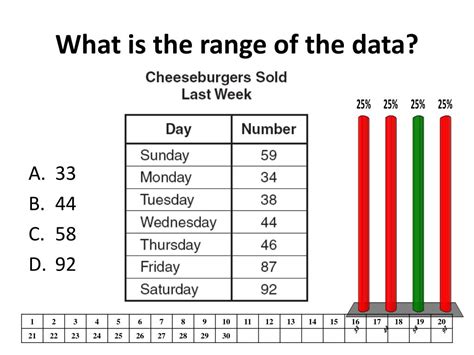
Table of Contents
Determining the Range of Data: A Comprehensive Guide
Understanding the range of your data is a fundamental step in any statistical analysis. The range, simply put, is the difference between the highest and lowest values in a dataset. While seemingly straightforward, grasping the nuances of range calculation and interpretation, particularly within diverse datasets, is crucial for drawing meaningful conclusions. This article delves into the intricacies of determining the range, exploring its applications, limitations, and implications for various analytical scenarios.
What is the Range?
The range is a descriptive statistic that measures the spread or dispersion of a dataset. It provides a quick snapshot of the variability present within the data. Calculating the range involves subtracting the minimum value from the maximum value. The result indicates the total span of values covered by the dataset. For example, if your data set includes values ranging from 10 to 50, the range is 40 (50-10).
Formula:
Range = Maximum Value - Minimum Value
This seemingly simple formula holds significant value in various applications, offering valuable insights into data distribution and characteristics.
Calculating the Range: A Step-by-Step Guide
Calculating the range is straightforward, but accuracy is paramount. Following these steps ensures a precise calculation:
-
Identify the Maximum Value: Scan your dataset to pinpoint the highest value present.
-
Identify the Minimum Value: Similarly, find the lowest value within your dataset.
-
Subtract the Minimum from the Maximum: Perform the subtraction as described in the formula above. The result is the range of your data.
Example:
Let's consider a dataset representing the daily temperatures (in degrees Celsius) for a week: 25, 28, 22, 30, 26, 24, 29.
- Maximum Value: 30°C
- Minimum Value: 22°C
- Range: 30°C - 22°C = 8°C
Therefore, the range of daily temperatures is 8°C.
Applications of the Range
The range, despite its simplicity, finds applications in diverse fields:
-
Quality Control: In manufacturing, the range helps monitor the variability of product dimensions or characteristics. A large range may indicate inconsistent production processes requiring attention.
-
Finance: Analyzing the range of stock prices over a period helps assess the volatility of an investment. A wide range often suggests higher risk.
-
Environmental Science: Determining the range of pollutant concentrations helps understand the extent of environmental contamination.
-
Healthcare: The range of patient blood pressure readings provides insight into the variability of health conditions.
-
Education: Analyzing the range of test scores within a classroom highlights the spread of student performance.
Limitations of the Range
While useful, the range has limitations:
-
Sensitivity to Outliers: The range is highly sensitive to extreme values or outliers. A single unusually high or low value can significantly inflate the range, skewing the perception of data variability. This makes the range less reliable when outliers are present.
-
Limited Information: The range only considers the two most extreme values, ignoring the distribution of the remaining data points. It doesn't reveal how the data is clustered or distributed within the range. For example, two datasets with the same range can have vastly different distributions.
-
Inappropriate for Skewed Data: In datasets with skewed distributions (where the data is concentrated towards one end of the range), the range might not be a suitable measure of variability. Other measures, like the interquartile range (IQR), are more robust in such scenarios.
Alternatives to the Range
When the limitations of the range become problematic, consider alternative measures of dispersion:
-
Interquartile Range (IQR): The IQR is the difference between the third quartile (75th percentile) and the first quartile (25th percentile) of a dataset. It's less susceptible to the influence of outliers than the range.
-
Variance and Standard Deviation: Variance and standard deviation measure the average squared deviation of data points from the mean. They provide a more comprehensive picture of data variability than the range.
-
Mean Absolute Deviation (MAD): MAD calculates the average absolute deviation of data points from the mean. It's a less complex alternative to variance and standard deviation.
Interpreting the Range in Context
The interpretation of the range depends heavily on the context of the data. A large range might be expected in some situations, while a small range might be considered significant in others. Consider these factors:
-
Units of Measurement: The numerical value of the range is meaningful only within the context of the units used. A range of 10 in kilometers is vastly different from a range of 10 in millimeters.
-
Data Type: The interpretation of the range varies depending on whether the data is continuous, discrete, or categorical.
-
Sample Size: The range calculated from a small sample size might not accurately represent the population range.
-
Data Distribution: Understanding the shape of the data distribution (e.g., normal, skewed) helps in interpreting the range more effectively.
Advanced Applications and Considerations
Understanding the range extends beyond simple calculations. Here are some advanced considerations:
-
Data Transformation: Before calculating the range, consider if data transformation (e.g., logarithmic transformation) is necessary to address skewness or stabilize variance.
-
Range in Multidimensional Data: In datasets with multiple variables, the range can be calculated for each variable individually, offering insights into the variability along each dimension.
-
Range as a Tool for Outlier Detection: While sensitive to outliers, the range can serve as a preliminary tool for identifying potential outliers. Values far beyond the range's boundaries warrant further investigation.
-
Range in Time Series Analysis: In time-series data, the range can be calculated for specific periods, revealing changes in variability over time.
Conclusion
The range, despite its simplicity, remains a valuable tool for understanding data variability. While its limitations should be considered, and alternatives explored where appropriate, the range offers a quick and easily understood measure of spread. By understanding its calculation, applications, limitations, and the importance of contextual interpretation, you gain a crucial skill for analyzing and interpreting data effectively, paving the way for more insightful statistical analysis. Remember to consider the overall context and distribution of your data to ensure the range provides a meaningful representation of its variability. Always be mindful of outliers and consider more robust measures of dispersion if necessary for a complete understanding of your data.
Latest Posts
Latest Posts
-
How Many Pi Bonds Are In A Triple Bond
Apr 05, 2025
-
How To Find Area Of Parallelogram With Vectors
Apr 05, 2025
-
Why Do Contour Lines Never Cross
Apr 05, 2025
-
Is Boron A Gas Solid Or Liquid
Apr 05, 2025
-
How Do You Factor 2x 2 7x 3
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about What Is The Range Of The Data Below . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
