What Is 4/2 In Simplest Form
listenit
May 25, 2025 · 6 min read
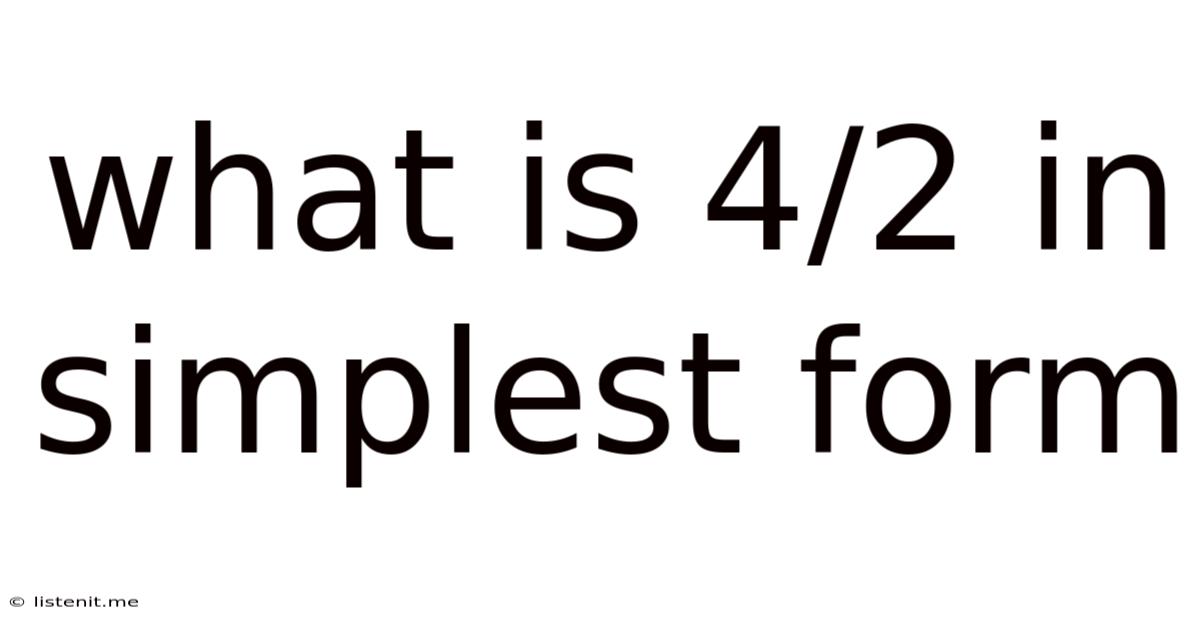
Table of Contents
What is 4/2 in Simplest Form? A Comprehensive Guide to Fraction Simplification
Understanding fractions is fundamental to mathematics, and simplifying them is a crucial skill. This comprehensive guide will explore the question, "What is 4/2 in simplest form?", delving into the process of fraction simplification and providing a solid foundation for tackling more complex fraction problems. We'll cover not only the solution but also the underlying principles and techniques applicable to various fraction scenarios.
Understanding Fractions
Before diving into simplification, let's briefly review what a fraction represents. A fraction is a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts you have, and the denominator indicates how many parts make up the whole. For instance, in the fraction 4/2, 4 is the numerator and 2 is the denominator.
Simplifying Fractions: The Concept of Equivalent Fractions
Simplifying a fraction means reducing it to its lowest terms. This doesn't change the fraction's value; it just represents it in a more concise and manageable form. We achieve this by finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by it.
Two fractions are considered equivalent if they represent the same value. For example, 1/2, 2/4, 3/6, and 4/8 are all equivalent fractions because they all represent half of a whole. Simplifying a fraction means finding the equivalent fraction with the smallest possible numerator and denominator.
Finding the Greatest Common Divisor (GCD)
The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. There are several ways to find the GCD:
1. Listing Factors:
This method involves listing all the factors of both the numerator and the denominator and identifying the largest factor they have in common.
For example, let's find the GCD of 12 and 18:
- Factors of 12: 1, 2, 3, 4, 6, 12
- Factors of 18: 1, 2, 3, 6, 9, 18
The largest common factor is 6. Therefore, the GCD of 12 and 18 is 6.
2. Prime Factorization:
This method involves expressing both the numerator and the denominator as a product of their prime factors. The GCD is then the product of the common prime factors raised to the lowest power.
Let's find the GCD of 12 and 18 using prime factorization:
- Prime factorization of 12: 2 x 2 x 3 (2² x 3)
- Prime factorization of 18: 2 x 3 x 3 (2 x 3²)
The common prime factors are 2 and 3. The lowest power of 2 is 2¹, and the lowest power of 3 is 3¹. Therefore, the GCD is 2 x 3 = 6.
3. Euclidean Algorithm:
This is a more efficient method for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
Let's find the GCD of 48 and 18 using the Euclidean algorithm:
- Divide 48 by 18: 48 = 2 x 18 + 12
- Divide 18 by the remainder 12: 18 = 1 x 12 + 6
- Divide 12 by the remainder 6: 12 = 2 x 6 + 0
The last non-zero remainder is 6, so the GCD of 48 and 18 is 6.
Simplifying 4/2
Now, let's apply these concepts to simplify 4/2.
First, we find the GCD of 4 and 2. Using any of the methods above (listing factors is easiest here):
- Factors of 4: 1, 2, 4
- Factors of 2: 1, 2
The GCD of 4 and 2 is 2.
Next, we divide both the numerator and the denominator by the GCD:
4 ÷ 2 = 2 2 ÷ 2 = 1
Therefore, 4/2 simplified to its lowest terms is 2/1.
Further Simplification and Representing Whole Numbers
While 2/1 is technically correct, it's also a whole number. Any fraction where the numerator is a multiple of the denominator can be expressed as a whole number or a mixed number. In this case:
2/1 = 2
This means that 4/2 represents two whole units.
Practical Applications and Real-World Examples
Understanding fraction simplification is crucial in numerous real-world scenarios. Here are a few examples:
-
Cooking and Baking: Recipes often require fractions of ingredients. Simplifying fractions helps you understand the proportions more easily. For instance, if a recipe calls for 4/2 cups of flour, you know you need 2 cups.
-
Measurement and Construction: In construction and engineering, accurate measurements are paramount. Simplifying fractions ensures precise calculations and avoids errors.
-
Data Analysis: In statistics and data analysis, simplifying fractions facilitates clearer interpretation of data and results.
-
Financial Calculations: Fractions are frequently used in financial calculations like calculating interest, profit margins, and shares. Simplifying them streamlines the calculations and helps in better decision-making.
-
Everyday Life: From dividing pizza slices fairly among friends to understanding discounts in shops, fraction simplification is frequently encountered in daily activities.
Expanding Your Knowledge: Working with More Complex Fractions
The principles of simplifying fractions remain the same regardless of the complexity of the numbers involved. Let's consider a few examples:
Example 1: Simplify 12/18
- Find the GCD of 12 and 18 (which we found earlier to be 6).
- Divide both numerator and denominator by 6: 12 ÷ 6 = 2 and 18 ÷ 6 = 3
- The simplified fraction is 2/3.
Example 2: Simplify 24/36
- Find the GCD of 24 and 36 (using prime factorization or the Euclidean algorithm, you'll find the GCD is 12).
- Divide both numerator and denominator by 12: 24 ÷ 12 = 2 and 36 ÷ 12 = 3
- The simplified fraction is 2/3.
Example 3: Simplify 105/135
- Find the GCD of 105 and 135 (using any method; the GCD is 15).
- Divide both numerator and denominator by 15: 105 ÷ 15 = 7 and 135 ÷ 15 = 9
- The simplified fraction is 7/9.
Conclusion: Mastering Fraction Simplification
Simplifying fractions is a fundamental mathematical skill with widespread applications. By understanding the concept of equivalent fractions, finding the greatest common divisor, and applying the steps outlined in this guide, you can confidently simplify any fraction to its simplest form. Remember, the goal is not just to get the right answer, but to understand the underlying principles and techniques that allow you to solve similar problems with ease and efficiency. This understanding empowers you to tackle more complex mathematical concepts and confidently apply your knowledge to various real-world scenarios. The seemingly simple question "What is 4/2 in simplest form?" opens the door to a deeper understanding of fractions and their vital role in mathematics and beyond.
Latest Posts
Latest Posts
-
100 Divided By What Equals 4
May 25, 2025
-
What Is The Gcf Of 16 24 And 40
May 25, 2025
-
Divide 6 13 By 6 12
May 25, 2025
-
1 5 3 4 As A Fraction
May 25, 2025
-
How To Round To The Nearest Foot
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 4/2 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.