1/5 + 3/4 As A Fraction
listenit
May 25, 2025 · 5 min read
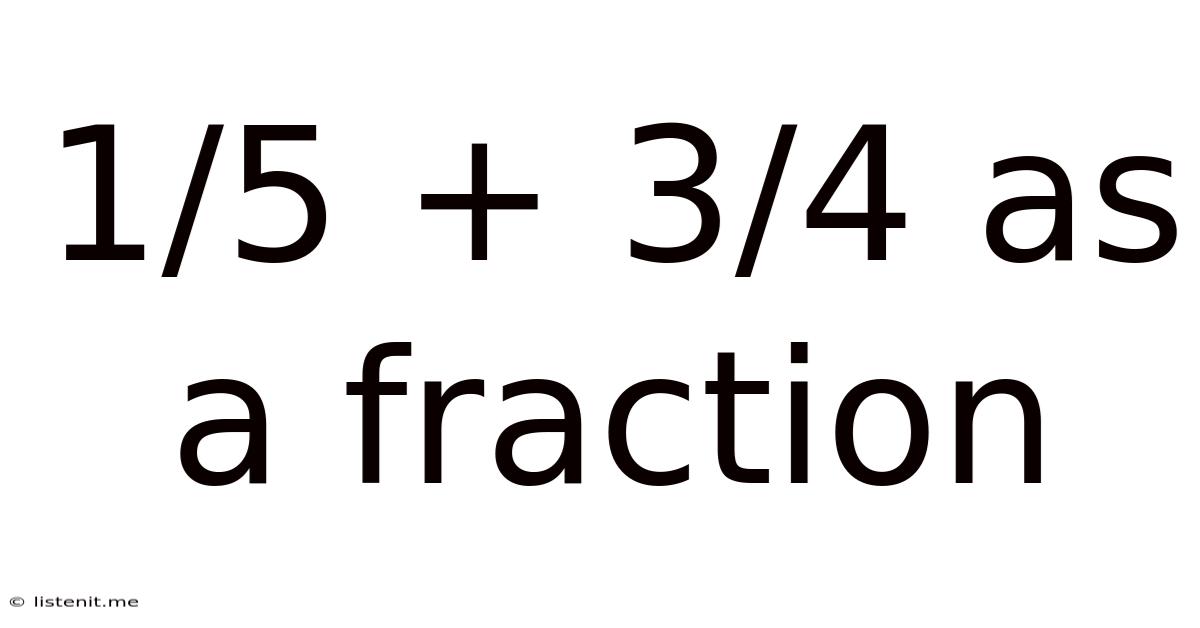
Table of Contents
1/5 + 3/4 as a Fraction: A Comprehensive Guide to Fraction Addition
Adding fractions might seem daunting at first, but with a systematic approach, it becomes straightforward. This comprehensive guide will walk you through the process of adding 1/5 and 3/4, explaining the underlying principles and providing practical examples to solidify your understanding. We'll delve into the concept of finding a common denominator, simplifying fractions, and ultimately arrive at the correct answer. By the end, you'll be confident in tackling similar fraction addition problems.
Understanding Fractions
Before we dive into the addition, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two main parts:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 1/5, the numerator is 1 (we have one part), and the denominator is 5 (the whole is divided into five equal parts). Similarly, in 3/4, the numerator is 3, and the denominator is 4.
Finding a Common Denominator
The crucial step in adding fractions is finding a common denominator. This is a number that is a multiple of both denominators. A common denominator allows us to express both fractions in terms of the same unit, making addition possible.
In our case, we need to find a common denominator for 5 and 4. One way to do this is to list the multiples of each number:
- Multiples of 5: 5, 10, 15, 20, 25, 30...
- Multiples of 4: 4, 8, 12, 16, 20, 24...
Notice that 20 appears in both lists. Therefore, 20 is a common denominator for 5 and 4. We could also use other common multiples like 40, 60, and so on, but using the least common denominator (LCD), which is the smallest common multiple, simplifies the calculations. In this case, the LCD is 20.
Converting Fractions to the Common Denominator
Now that we have a common denominator (20), we need to convert both fractions, 1/5 and 3/4, so they have this denominator. We achieve this by multiplying both the numerator and the denominator of each fraction by the appropriate number.
-
Converting 1/5: To get a denominator of 20, we need to multiply 5 by 4 (because 5 x 4 = 20). We must also multiply the numerator by 4 to maintain the fraction's value:
(1 x 4) / (5 x 4) = 4/20
-
Converting 3/4: To get a denominator of 20, we need to multiply 4 by 5 (because 4 x 5 = 20). Again, we multiply the numerator by 5:
(3 x 5) / (4 x 5) = 15/20
Now both fractions have the same denominator (20): 4/20 and 15/20.
Adding the Fractions
With both fractions having a common denominator, adding them is straightforward: we simply add the numerators and keep the denominator the same.
4/20 + 15/20 = (4 + 15) / 20 = 19/20
Therefore, 1/5 + 3/4 = 19/20.
Simplifying Fractions (If Necessary)
After adding fractions, it's essential to simplify the result if possible. A fraction is simplified when the numerator and denominator have no common factors other than 1. In our case, 19/20 is already in its simplest form because 19 is a prime number and doesn't share any factors with 20 other than 1.
Alternative Methods for Finding the Least Common Denominator (LCD)
While listing multiples works well for smaller numbers, it can become cumbersome with larger numbers. Here are two more efficient methods for finding the LCD:
1. Prime Factorization Method
This method involves finding the prime factorization of each denominator. The LCD is the product of the highest powers of all prime factors present in the denominators.
- Prime factorization of 5: 5 (5 is a prime number)
- Prime factorization of 4: 2 x 2 = 2²
The prime factors are 2 and 5. The highest power of 2 is 2², and the highest power of 5 is 5¹. Therefore, the LCD is 2² x 5 = 4 x 5 = 20.
2. Greatest Common Divisor (GCD) Method
This method utilizes the GCD (greatest common divisor) of the denominators. The LCD can be calculated using the formula:
LCD(a, b) = (a x b) / GCD(a, b)
where 'a' and 'b' are the denominators.
- In our case, a = 5 and b = 4.
- The GCD of 5 and 4 is 1 (they share no common factors other than 1).
- Therefore, LCD(5, 4) = (5 x 4) / 1 = 20
Practical Applications of Fraction Addition
Adding fractions is not just an abstract mathematical concept; it has numerous practical applications in daily life. Consider these examples:
-
Cooking and Baking: Recipes often require fractions of ingredients. Adding fractions is crucial for accurately calculating the total amount of an ingredient needed when combining recipes or adjusting serving sizes.
-
Construction and Engineering: Precise measurements are vital in construction and engineering. Adding fractions is essential when calculating dimensions, material quantities, and distances.
-
Finance and Budgeting: Managing finances often involves dealing with fractions of monetary units (e.g., cents). Adding fractions is necessary for tracking expenses, calculating interest, and budgeting effectively.
-
Data Analysis: In data analysis and statistics, fractions are used to represent proportions and probabilities. Adding fractions is a fundamental step in many statistical calculations.
Troubleshooting Common Mistakes
Here are some common mistakes to avoid when adding fractions:
-
Adding numerators and denominators directly: Remember, you cannot simply add the numerators and denominators directly. You must find a common denominator first.
-
Incorrectly converting to the common denominator: Always multiply both the numerator and the denominator by the same number when converting fractions to a common denominator. Multiplying only the numerator or denominator will change the value of the fraction.
-
Forgetting to simplify: Always simplify the resulting fraction to its lowest terms to obtain the most concise representation.
Conclusion
Adding fractions, although seemingly complex at first glance, is a fundamental mathematical operation with widespread applications. By understanding the principles of finding a common denominator, converting fractions, and simplifying results, you can confidently tackle any fraction addition problem. Remember to practice regularly to solidify your understanding and improve your speed and accuracy. This detailed guide has equipped you with the necessary knowledge and techniques to master fraction addition. Now, go forth and conquer those fractions!
Latest Posts
Latest Posts
-
Calculate Calories Burned By Heart Rate
May 25, 2025
-
What Size Ac Unit For 400 Square Feet
May 25, 2025
-
1 Out Of 30 As A Percentage
May 25, 2025
-
Whats A 6 Out Of 10
May 25, 2025
-
Where Can I Buy A Weight Watchers Calculator
May 25, 2025
Related Post
Thank you for visiting our website which covers about 1/5 + 3/4 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.