100 Divided By What Equals 4
listenit
May 25, 2025 · 5 min read
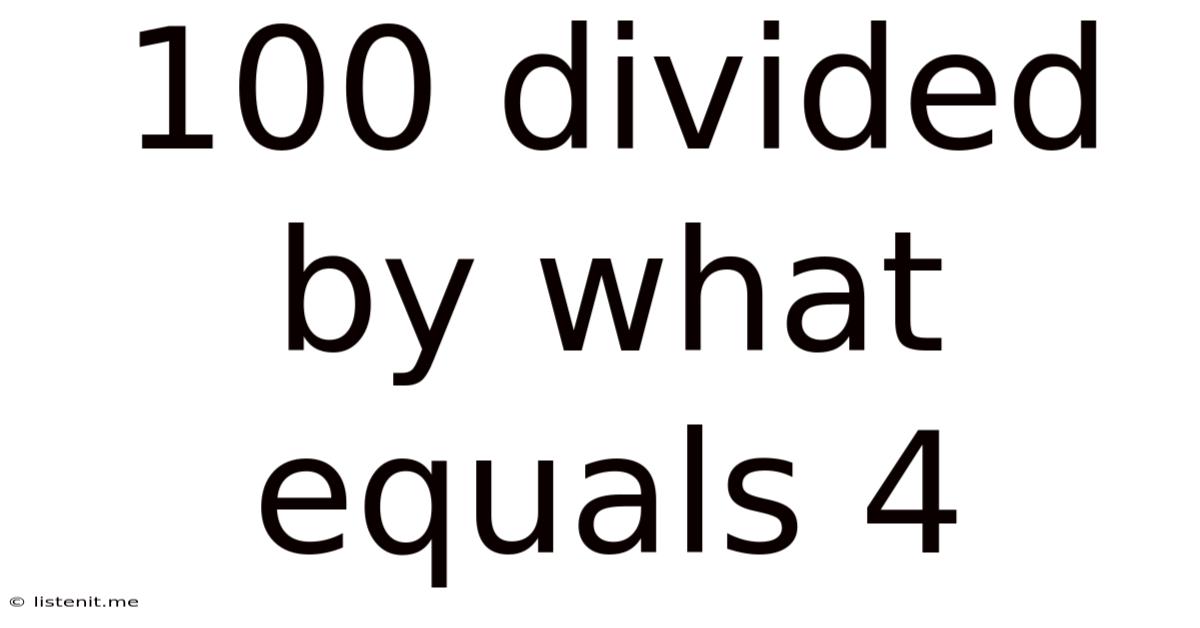
Table of Contents
100 Divided by What Equals 4: A Deep Dive into Division and Problem-Solving
The seemingly simple question, "100 divided by what equals 4?", opens a door to a fascinating exploration of division, mathematical problem-solving, and even the practical applications of these concepts in everyday life. While the immediate answer might be readily apparent to many, delving deeper reveals a wealth of understanding about fundamental mathematical principles and their broader implications. This article will not only answer the question directly but also explore the underlying concepts, different approaches to solving the problem, and related mathematical ideas.
Understanding the Problem: Deconstructing 100 ÷ x = 4
The core of the problem lies in understanding the equation: 100 ÷ x = 4. This equation represents a division problem where we are seeking the unknown value, 'x', that, when 100 is divided by it, results in a quotient of 4. This is a fundamental algebraic equation, and understanding how to solve it unlocks the ability to solve countless similar problems.
Key Terms and Concepts
Before proceeding, let's solidify our understanding of some key terms:
- Dividend: The number being divided (in this case, 100).
- Divisor: The number by which the dividend is divided (the unknown 'x' in our equation).
- Quotient: The result of the division (in this case, 4).
- Algebraic Equation: An equation containing one or more variables (like 'x') which represent unknown quantities.
Understanding these terms is crucial for tackling not only this specific problem but also a broad range of mathematical equations.
Solving the Equation: Finding the Value of 'x'
There are several ways to solve the equation 100 ÷ x = 4. Let's explore two common approaches:
Method 1: Using Inverse Operations
The most straightforward method involves using inverse operations. Division and multiplication are inverse operations; they undo each other. To isolate 'x', we can multiply both sides of the equation by 'x':
100 ÷ x = 4
x * (100 ÷ x) = 4 * x
100 = 4x
Now, we divide both sides by 4 to solve for 'x':
100/4 = x
x = 25
Therefore, 100 divided by 25 equals 4.
Method 2: Cross-Multiplication (for Ratios)
While less direct for this specific problem, framing the equation as a ratio provides an alternative solution. We can rewrite the equation as:
100/x = 4/1
This represents a proportion. Cross-multiplication provides a solution:
100 * 1 = 4 * x
100 = 4x
Dividing both sides by 4 again yields:
x = 25
This demonstrates the versatility of different mathematical approaches to arrive at the same solution.
Beyond the Answer: Exploring Related Concepts
Solving "100 divided by what equals 4" is only the first step. Understanding the underlying mathematical concepts broadens our problem-solving capabilities. Let's explore some related ideas:
Fractions and Division
Division is intrinsically linked to fractions. The equation 100 ÷ 25 = 4 can be expressed as the fraction 100/25. Simplifying this fraction leads directly to the answer:
100/25 = 4/1 = 4
This emphasizes the interconnectedness of different mathematical representations.
Real-World Applications
The principles of division find numerous applications in everyday life:
- Sharing Resources: Dividing 100 cookies among 25 friends.
- Calculating Unit Prices: Determining the price per item if 100 items cost $400.
- Scaling Recipes: Adjusting ingredient quantities in a recipe.
- Data Analysis: Calculating averages or proportions in datasets.
The ability to solve equations like 100 ÷ x = 4 is fundamental to many practical situations.
Expanding the Concept: Solving More Complex Equations
Once we understand the fundamental principle, we can tackle more complex equations involving division. For instance, consider:
200 ÷ (x + 5) = 10
Solving this requires a multi-step process involving inverse operations and algebraic manipulation. This builds upon the basic principles established by solving the simpler equation.
Problem-Solving Strategies and Techniques
Let's further delve into strategies that enhance mathematical problem-solving skills, going beyond simply finding the solution to "100 divided by what equals 4."
1. Visual Representation
Visual aids can greatly simplify the understanding and solving of mathematical problems. For the problem at hand, imagining 100 objects being divided into groups of 4 can help visualize the solution. This approach can be particularly helpful for those who prefer a more concrete, less abstract understanding of mathematical concepts.
2. Breaking Down Complex Problems
When confronted with more intricate mathematical equations, breaking them down into smaller, more manageable parts is crucial. This step-by-step approach minimizes the risk of errors and increases the likelihood of obtaining the correct solution. It’s similar to assembling a puzzle; each step brings you closer to the complete picture.
3. Checking Your Work
Once a solution is obtained, it's imperative to check the work. This process verifies the accuracy of the solution and reinforces understanding. Substituting the obtained value of 'x' back into the original equation, 100 ÷ x = 4, ensures the equation holds true. This habit builds confidence and precision in problem-solving.
4. Utilizing Different Methods
Proficiency in math often involves understanding multiple methods for achieving the same result. As shown earlier, both the inverse operation method and the ratio/cross-multiplication method successfully solved the equation. This flexibility provides alternative approaches if one method proves challenging or inefficient.
5. Practice and Persistence
Consistent practice is paramount to improving mathematical skills. Regularly engaging with various problem-solving exercises solidifies the understanding of core concepts and increases confidence in tackling more complex equations. Persistence is key; challenges will arise, but perseverance will lead to improved mathematical fluency.
Conclusion: Beyond the Numbers
The seemingly simple question, "100 divided by what equals 4?", serves as a springboard for exploring fundamental mathematical principles, problem-solving strategies, and real-world applications. The answer, 25, is only a small part of the larger picture. Understanding the underlying concepts, exploring different solution methods, and developing effective problem-solving strategies are far more valuable in the long run. This journey through division underscores the beauty and practical utility of mathematics in our daily lives. By mastering these fundamental concepts, we equip ourselves with the tools to tackle more complex mathematical challenges and gain a deeper appreciation for the logic and elegance of mathematics.
Latest Posts
Latest Posts
-
What Is 12 49 Rounded To The Nearest Integer
May 25, 2025
-
How Much Is A 70 Percent Grade
May 25, 2025
-
What Is The Prime Factorization Of 87
May 25, 2025
-
What Is 1 X 1 2
May 25, 2025
-
What Is 48 Minutes From Now
May 25, 2025
Related Post
Thank you for visiting our website which covers about 100 Divided By What Equals 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.