What Is 1 X 1 2
listenit
May 25, 2025 · 5 min read
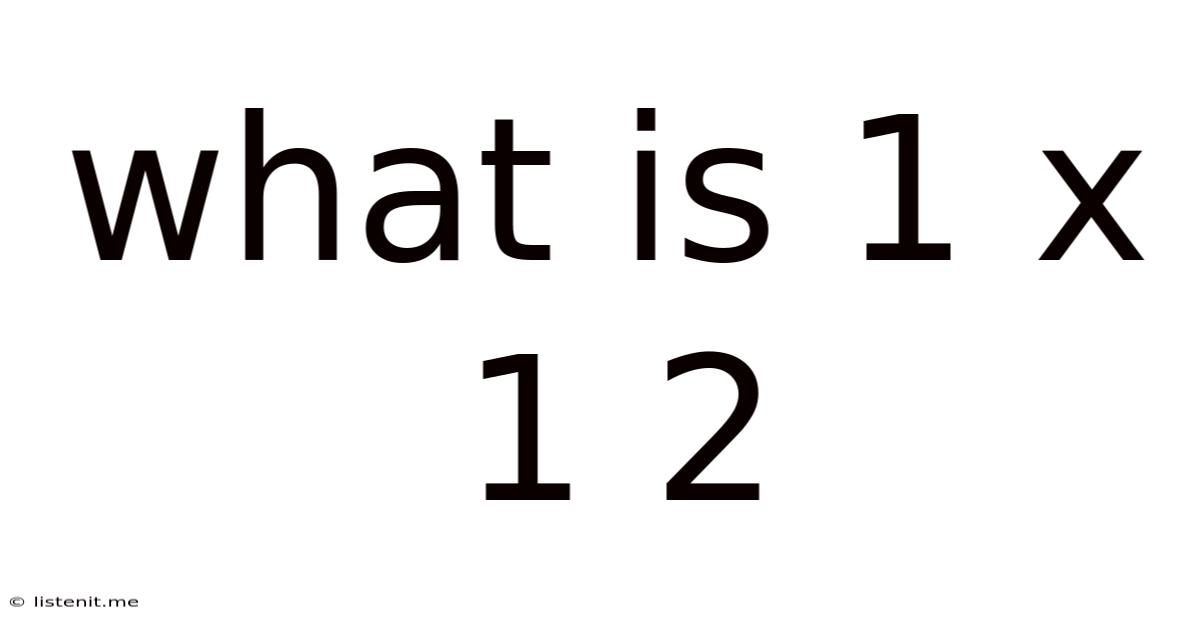
Table of Contents
What is 1 x 1 2? Decoding the Enigma of Mathematical Notation
The seemingly simple expression "1 x 1 2" presents a fascinating puzzle, highlighting the importance of precise mathematical notation and the potential for ambiguity when such precision is lacking. While at first glance, it might appear straightforward, its interpretation hinges on the understanding of order of operations and the subtle nuances of mathematical symbolism. This article delves into the various possible interpretations of "1 x 1 2," explores the fundamental principles that govern mathematical calculations, and underscores the critical role of clear communication in mathematics.
The Importance of Order of Operations (PEMDAS/BODMAS)
The core of understanding "1 x 1 2" lies in the principle of order of operations, often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). These mnemonics dictate the sequence in which operations should be performed within a mathematical expression to arrive at a consistent and unambiguous result.
Without specifying parentheses or using explicit multiplication symbols, the expression "1 x 1 2" leaves room for different interpretations:
-
Interpretation 1: (1 x 1) 2 Following PEMDAS/BODMAS strictly, multiplication is performed before any implicit multiplication indicated by the juxtaposition of numbers. This interpretation leads to:
- (1 x 1) = 1
- 1 x 2 = 2
- Therefore, (1 x 1) 2 = 2
-
Interpretation 2: 1 x (12) Here, we assume that "12" represents a single number, implicitly multiplying 1 by 12. This interpretation results in:
- 1 x 12 = 12
- Therefore, 1 x (12) = 12
The discrepancy between these interpretations underscores the crucial role of clear mathematical notation. Ambiguity can lead to errors and miscommunication, particularly in complex calculations.
The Role of Explicit Multiplication Symbols
Using explicit multiplication symbols (like 'x' or '*') clarifies the intended operation. For example:
- 1 x 1 x 2 unequivocally results in 2.
- 1 x 12 clearly produces 12.
The absence of explicit symbols, especially the lack of a multiplication symbol between 1 and 2 in the original expression "1 x 1 2", fuels the ambiguity. This is why, in advanced mathematical contexts, the use of explicit symbols is strongly encouraged to avoid any misinterpretation.
Implicit Multiplication and Juxtaposition
The expression "1 x 1 2" also highlights the concept of implicit multiplication (where multiplication is implied without an explicit symbol, often through juxtaposition—placing numbers side-by-side). In many programming languages and advanced mathematical texts, implicit multiplication, especially when involving variables or parentheses, often takes precedence over explicit multiplication signs. However, this priority is context-dependent and may not always apply universally, making consistency in notation paramount.
Understanding Different Mathematical Contexts
The interpretation of "1 x 1 2" could also depend on the specific mathematical context where it is encountered. For instance, in certain programming languages, the interpretation might differ based on the compiler or interpreter used. This underscores the importance of understanding the specific rules and conventions of the given context.
The Importance of Clear Communication in Mathematics
Beyond the order of operations, the incident with "1 x 1 2" emphasizes the broader importance of clear and unambiguous communication in mathematics. Precise notation is not merely a stylistic preference but a fundamental requirement for accurate calculations, efficient problem-solving, and effective communication among mathematicians, scientists, programmers, and anyone who uses mathematics.
Avoiding Ambiguity: Best Practices in Mathematical Notation
To prevent misunderstandings, several best practices can be followed when writing mathematical expressions:
- Use parentheses liberally: Parentheses clearly group operations, eliminating ambiguity about the order of execution. Even when following PEMDAS/BODMAS strictly, using parentheses can improve readability and reduce the risk of errors.
- Use explicit multiplication symbols: Never rely solely on juxtaposition to imply multiplication, particularly when dealing with numbers and variables. Explicit symbols ('x', '*', or a centered dot '⋅') significantly reduce the chance of misinterpretation.
- Maintain consistent notation: Choose a notation style and adhere to it consistently throughout the expression or document. This ensures that the intended meaning is clear and predictable.
- Check your work: After writing a mathematical expression, double-check it to ensure that the notation is unambiguous and that the order of operations is correctly represented.
Extending the Concept: Complex Mathematical Expressions
The insights gained from analyzing "1 x 1 2" extend to more complex mathematical expressions. Consider expressions involving exponents, fractions, roots, and various functions. The principles of order of operations and clear notation remain equally vital in navigating these more intricate calculations.
Implications in Programming and Computer Science
In the field of programming, the order of operations is critical, and each programming language may have slightly different rules regarding operator precedence. The interpretation of "1 x 1 2" (or its equivalent in code) would depend entirely on the language's rules for operator precedence and the use of implicit multiplication. Understanding this language-specific behavior is crucial for programmers to avoid unexpected results and bugs in their code.
Conclusion: The Value of Precision in Mathematics
The seemingly simple expression "1 x 1 2" serves as a potent reminder of the significance of precise mathematical notation and the strict adherence to the order of operations. Ambiguity, often arising from the lack of explicit symbols or an inconsistent application of mathematical rules, can lead to incorrect results and miscommunication. By emphasizing the use of parentheses, explicit multiplication symbols, and consistent notation, we can significantly enhance the clarity and accuracy of mathematical expressions, fostering a stronger understanding and application of mathematics across various disciplines. The puzzle of "1 x 1 2" underscores the importance of precision not just as a stylistic choice but as a fundamental pillar of mathematical integrity. Mastering these principles contributes to successful problem-solving and clear communication in the world of mathematics and beyond.
Latest Posts
Latest Posts
-
Buy 2 Get 1 Free Discount Percentage
May 25, 2025
-
3 4 Plus 3 4 Equals In Cups
May 25, 2025
-
3 3 6 As An Improper Fraction
May 25, 2025
-
7 12 Divided By 5 9 In Fraction Form
May 25, 2025
-
30 Days From October 1st 2024
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 X 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.