7/12 Divided By 5/9 In Fraction Form
listenit
May 25, 2025 · 4 min read
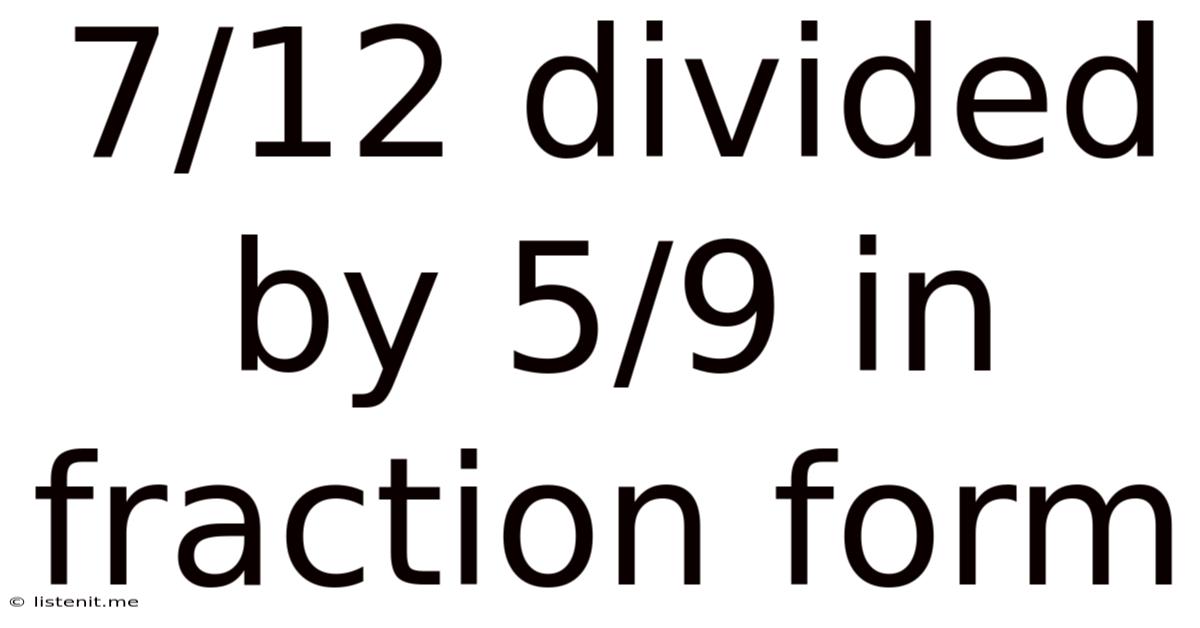
Table of Contents
7/12 Divided by 5/9 in Fraction Form: A Comprehensive Guide
Dividing fractions can seem daunting at first, but with a clear understanding of the process, it becomes straightforward. This comprehensive guide will walk you through dividing 7/12 by 5/9, explaining the steps involved, providing alternative methods, and exploring related concepts to solidify your understanding of fraction division.
Understanding Fraction Division
Before diving into the specific problem, let's review the fundamental principle of dividing fractions. The core concept is to invert the second fraction (the divisor) and multiply it by the first fraction (the dividend). This process is often summarized as "keep, change, flip".
- Keep: Keep the first fraction as it is.
- Change: Change the division sign to a multiplication sign.
- Flip: Flip (or invert) the second fraction, swapping the numerator and denominator.
Solving 7/12 Divided by 5/9
Now, let's apply this principle to solve 7/12 divided by 5/9:
-
Keep: We keep the first fraction, 7/12, unchanged.
-
Change: We change the division sign (÷) to a multiplication sign (×).
-
Flip: We invert the second fraction, 5/9, becoming 9/5.
This transforms the problem into:
(7/12) × (9/5)
Performing the Multiplication
Multiplying fractions is relatively simple. We multiply the numerators together and the denominators together:
Numerator: 7 × 9 = 63
Denominator: 12 × 5 = 60
This gives us the result: 63/60
Simplifying the Fraction
The fraction 63/60 is not in its simplest form. To simplify, we need to find the greatest common divisor (GCD) of the numerator (63) and the denominator (60). The GCD of 63 and 60 is 3. We divide both the numerator and the denominator by 3:
63 ÷ 3 = 21
60 ÷ 3 = 20
Therefore, the simplified fraction is 21/20.
Representing the Answer as a Mixed Number
The fraction 21/20 is an improper fraction (the numerator is larger than the denominator). We can convert this into a mixed number, which consists of a whole number and a proper fraction.
To do this, we divide the numerator (21) by the denominator (20):
21 ÷ 20 = 1 with a remainder of 1
This means that 21/20 is equal to 1 and 1/20 (or 1 1/20).
Alternative Methods
While the "keep, change, flip" method is the most common, there are alternative approaches to dividing fractions that can enhance understanding:
Method 1: Using Common Denominators
This method involves finding a common denominator for both fractions before dividing. However, this approach is generally less efficient than the "keep, change, flip" method, especially for more complex problems.
Method 2: Visual Representation
Visualizing the division of fractions using models, such as area models or fraction circles, can be helpful, particularly for beginners. This method allows for a more intuitive understanding of the process.
Practical Applications
Understanding fraction division is crucial in many real-world scenarios:
- Cooking and Baking: Scaling recipes up or down requires dividing fractions.
- Sewing and Crafts: Calculating fabric requirements or cutting precise measurements involves fraction division.
- Construction and Engineering: Precise measurements and calculations in construction and engineering often necessitate fraction division.
- Data Analysis: Working with proportions and percentages often involves fraction division.
Expanding on Fraction Concepts
Let's delve deeper into some related concepts to further solidify your understanding of fractions:
Greatest Common Divisor (GCD)
Finding the GCD is essential for simplifying fractions. There are several methods for finding the GCD, including the Euclidean algorithm and prime factorization. Understanding GCD helps in simplifying complex calculations and representing fractions in their most concise form.
Least Common Multiple (LCM)
The LCM is crucial when adding or subtracting fractions with different denominators. Finding the LCM allows you to rewrite fractions with a common denominator, facilitating the addition or subtraction process.
Improper Fractions and Mixed Numbers
Understanding the difference between improper fractions and mixed numbers is vital for accurate calculations and clear representation of results. Converting between these forms is a necessary skill for working with fractions effectively.
Equivalent Fractions
Recognizing equivalent fractions is crucial for simplification and comparison. Understanding how to find equivalent fractions ensures that you can work with different representations of the same value.
Conclusion
Dividing 7/12 by 5/9 results in 21/20, or 1 1/20, when simplified. Mastering fraction division is a crucial skill with wide-ranging applications. By understanding the fundamental principle of "keep, change, flip" and exploring alternative methods, you can confidently tackle fraction division problems and expand your mathematical abilities. Furthermore, delving into related concepts like GCD, LCM, and equivalent fractions solidifies your understanding and enhances your ability to work with fractions in various contexts. Remember, practice is key – the more you work with fractions, the more comfortable and proficient you will become.
Latest Posts
Latest Posts
-
How Many Days In 3 Year
May 25, 2025
-
30 Days After November 22 2024
May 25, 2025
-
What Is 8 15 As A Grade
May 25, 2025
-
What Percent Is 14 Of 24
May 25, 2025
-
6 Years Is How Many Days
May 25, 2025
Related Post
Thank you for visiting our website which covers about 7/12 Divided By 5/9 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.