What Percent Is 14 Of 24
listenit
May 25, 2025 · 4 min read
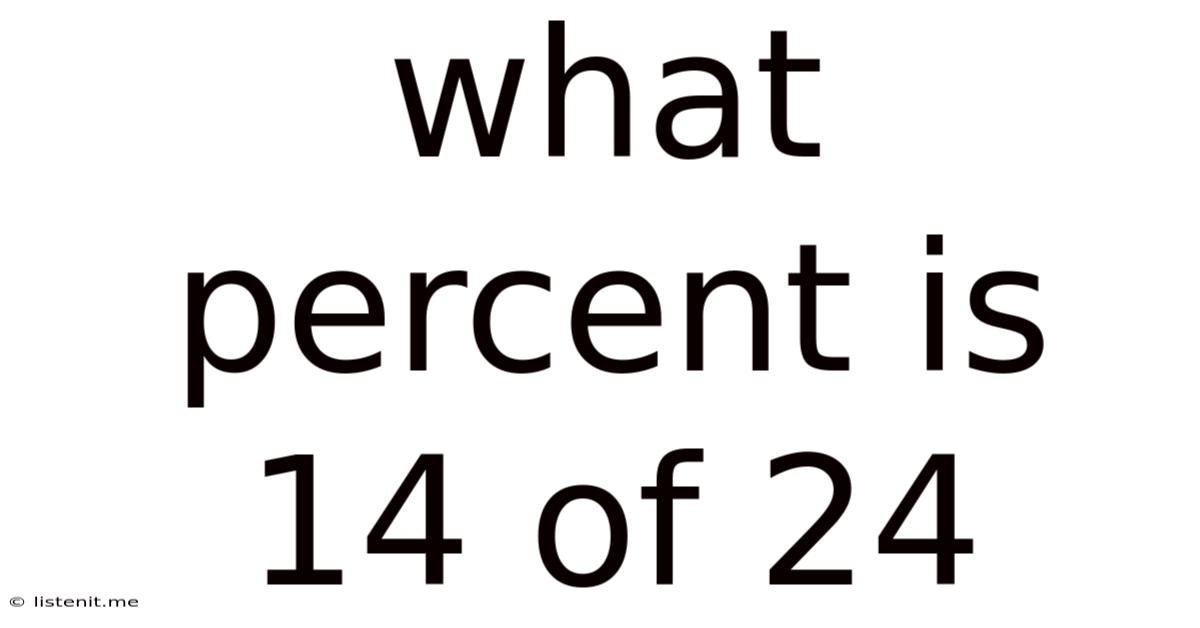
Table of Contents
What Percent is 14 of 24? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting and shopping to complex scientific analyses and financial modeling. Understanding how to determine what percent one number represents of another is crucial for interpreting data, making informed decisions, and generally navigating the numerical world around us. This article delves into the question, "What percent is 14 of 24?", providing a detailed explanation of the calculation process, exploring related concepts, and offering practical applications.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally translates to "out of one hundred." We use the symbol "%" to represent percentages. For instance, 50% means 50 out of 100, which is equivalent to ½ or 0.5.
Calculating "What Percent is 14 of 24?"
To determine what percentage 14 represents of 24, we follow these steps:
Step 1: Set up the Proportion
We can represent this problem as a proportion:
14/24 = x/100
Where:
- 14 is the part.
- 24 is the whole.
- x is the percentage we want to find.
Step 2: Solve for x
To solve for x, we cross-multiply:
14 * 100 = 24 * x
1400 = 24x
Step 3: Isolate x
Divide both sides of the equation by 24:
x = 1400 / 24
x ≈ 58.33
Therefore, 14 is approximately 58.33% of 24.
Alternative Calculation Methods
While the proportion method is straightforward, there are other ways to calculate percentages:
Method 1: Using Decimal Conversion
- Divide the part (14) by the whole (24): 14 ÷ 24 ≈ 0.5833
- Multiply the result by 100 to express it as a percentage: 0.5833 * 100 ≈ 58.33%
Method 2: Using a Calculator
Most calculators have a percentage function. Simply enter 14 ÷ 24 and then multiply by 100.
Practical Applications of Percentage Calculations
Understanding percentage calculations has far-reaching practical applications. Here are some examples:
-
Finance: Calculating interest rates, discounts, tax rates, profit margins, and investment returns all rely on percentage calculations. For instance, if a store offers a 20% discount on an item, knowing how to calculate that discount is essential.
-
Statistics: Percentages are fundamental in statistical analysis, allowing us to represent data proportions, trends, and probabilities effectively. Survey results, election polls, and scientific experiments often present findings as percentages.
-
Science: In scientific research, percentages are used to express concentrations, yields, and error margins. For example, the percentage of a particular element in a compound or the percentage error in a scientific experiment.
-
Everyday Life: Calculating tips in restaurants, understanding sale prices, determining the percentage of completion on a project, or analyzing nutritional information on food labels all involve percentage calculations.
-
Education: Grading systems, test scores, and class performance are commonly expressed as percentages.
Expanding on Percentage Concepts
Beyond the basic calculation, let's explore some related percentage concepts:
1. Percentage Increase and Decrease:
Calculating percentage changes is crucial for understanding growth or decline in various contexts. The formula for percentage increase or decrease is:
[(New Value - Old Value) / Old Value] * 100
For example, if the price of a product increases from $20 to $25, the percentage increase is:
[(25 - 20) / 20] * 100 = 25%
2. Percentage Points:
It's crucial to differentiate between percentage points and percentage changes. A percentage point refers to the absolute difference between two percentages. For instance, if interest rates increase from 5% to 8%, the increase is 3 percentage points, not 60% (which would be the percentage change).
3. Compounding Percentages:
In scenarios like compound interest, percentages are applied repeatedly. Understanding how compounding works is crucial for long-term financial planning.
Troubleshooting Common Percentage Calculation Mistakes
Several common mistakes can occur when calculating percentages:
-
Incorrectly Identifying the Part and the Whole: Ensuring you correctly identify which number represents the "part" and which represents the "whole" is crucial for accurate calculations.
-
Mixing Up Decimal Places: Errors can occur during decimal conversions or when performing calculations involving decimal numbers. Always double-check your calculations to avoid these errors.
-
Misinterpreting Percentage Points: Confusing percentage points with percentage changes can lead to incorrect interpretations and conclusions.
-
Failing to Account for Rounding: When dealing with non-whole numbers, rounding may be necessary. Be aware of how rounding might impact your final result and choose appropriate rounding strategies.
Advanced Percentage Applications
The principles of percentage calculation extend to more advanced applications:
-
Weighted Averages: In situations where different data points have different weights, weighted averages utilize percentages to account for these varying weights.
-
Statistical Inference: Percentages play a crucial role in statistical inference, enabling us to draw conclusions about populations based on sample data.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations empowers you to tackle a wide range of problems across diverse domains. From daily financial decisions to sophisticated statistical analysis, a solid understanding of percentages is essential. By practicing the various methods outlined in this article, paying close attention to detail, and avoiding common pitfalls, you can confidently and accurately calculate percentages in any situation. Remember, consistent practice is key to building proficiency in this fundamental skill. The more you practice, the more comfortable and accurate you will become with percentage calculations.
Latest Posts
Latest Posts
-
9 1 100 As A Decimal
May 26, 2025
-
Greatest Common Factor Of 21 And 36
May 26, 2025
-
Whats 40 Percent Off Of 50
May 26, 2025
-
1200 Btu Air Conditioner Room Size
May 26, 2025
-
Write 8 4 5 As A Decimal Number
May 26, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 14 Of 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.