3 4 Plus 3 4 Equals In Cups
listenit
May 25, 2025 · 6 min read
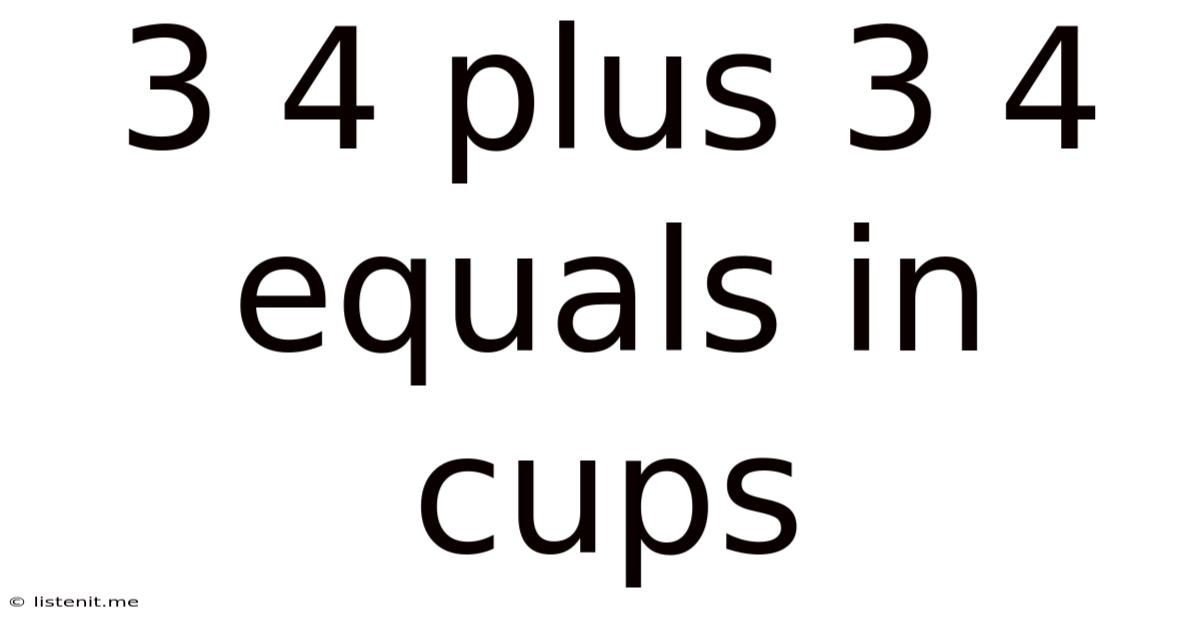
Table of Contents
Decoding the Culinary Conundrum: 3/4 Plus 3/4 Equals in Cups
Baking and cooking often require precision, and understanding fractional measurements is crucial for achieving consistent, delicious results. One common question that arises, particularly for those new to the kitchen, is: what does 3/4 plus 3/4 equal in cups? This seemingly simple question can be surprisingly complex, especially when considering practical applications in recipes. Let’s delve into this, explore different scenarios, and learn how to confidently handle fractional measurements in your culinary adventures.
Understanding Fractions in Cooking
Before tackling the main question, let's solidify our understanding of fractions. A fraction represents a part of a whole. In cooking, the "whole" is typically a cup, a tablespoon, or a teaspoon. The numerator (top number) indicates the number of parts we have, and the denominator (bottom number) indicates the total number of parts that make up the whole.
For example:
- 1/2 cup: This means we have one part out of two equal parts that make up a whole cup.
- 3/4 cup: This means we have three parts out of four equal parts that make up a whole cup.
Understanding this foundational concept is vital for accurately measuring ingredients and achieving the desired results in your recipes.
Solving 3/4 + 3/4
The mathematical solution to 3/4 + 3/4 is straightforward. We add the numerators (3 + 3 = 6) and keep the denominator the same (4). This gives us 6/4.
However, this is an improper fraction (where the numerator is larger than the denominator). To express this as a mixed number (a whole number and a fraction), we divide the numerator (6) by the denominator (4).
6 ÷ 4 = 1 with a remainder of 2.
Therefore, 6/4 is equal to 1 2/4.
We can further simplify 2/4 by dividing both the numerator and denominator by their greatest common divisor (2), resulting in 1/2.
So, the final answer is 1 1/2 cups.
Practical Applications in Recipes
Now that we know the mathematical answer, let's explore how this translates into practical cooking scenarios.
Imagine a recipe calls for 3/4 cup of butter and another 3/4 cup of sugar. Simply adding these fractions, as we did earlier, tells us that you need a total of 1 1/2 cups of butter and sugar combined. However, this doesn't necessarily mean you need one and a half measuring cups.
Here’s how you'd measure it practically:
- Use a 1-cup measuring cup: Fill it completely once.
- Use a 1/2-cup measuring cup: Fill it once to complete the 1 1/2 cups.
Variations and Considerations
While the basic calculation is simple, there are nuances to consider in practical cooking:
- Ingredient Density: The density of ingredients affects how accurately you can measure them. Dry ingredients like flour and sugar can settle differently, leading to slight variations in volume. Liquids, on the other hand, are generally easier to measure accurately.
- Recipe Variations: Some recipes may be flexible regarding minor variations in ingredient amounts. If the recipe involves multiple other ingredients, a small discrepancy in the total amount of butter and sugar likely won't significantly impact the final outcome.
- Rounded Measurements: Recipes often round off measurements for simplicity. A recipe might call for "about 1 ½ cups," giving you some leeway.
- Conversion to other units: Depending on the recipe, you might need to convert this measurement into other units, like milliliters or fluid ounces, using standard conversion charts.
Advanced Fractional Calculations in Baking
Let’s explore some more complex scenarios that could arise in recipes involving fractions:
Example 1: Adding different fractions.
A recipe calls for 1/4 cup of milk, 1/2 cup of oil, and 3/4 cup of water. To find the total amount of liquid, we need to add the fractions: 1/4 + 1/2 + 3/4
First, find a common denominator (4 works well in this case):
1/4 + 2/4 + 3/4 = 6/4 = 1 1/2 cups
Example 2: Subtracting fractions.
Let's say you started with 1 1/2 cups of flour, and your recipe requires you to use 3/4 cup. How much flour is left?
First, convert 1 1/2 cups to an improper fraction: (1 x 2 + 1) / 2 = 3/2
Now subtract 3/4 from 3/2. Find a common denominator (4):
6/4 - 3/4 = 3/4 cup of flour remaining.
Example 3: Multiplying fractions.
Suppose a recipe calls for half the amount of a particular ingredient, and that ingredient's original measurement was 3/4 cup. To find the required amount, multiply the fractions:
1/2 x 3/4 = 3/8 cup
Example 4: Dividing Fractions.
If a recipe calls for a specific amount of an ingredient, and you want to make half the recipe, you might need to divide the amount of the ingredient by 2.
For example, if you have 3/4 cup of sugar and need to make half the recipe, you will divide 3/4 by 2 (or multiply by 1/2):
(3/4) / 2 = (3/4) x (1/2) = 3/8 cup of sugar.
Mastering Fractions for Culinary Success
Understanding how to work with fractions is a crucial skill for any baker or cook. While initially it might seem daunting, with practice, it becomes second nature. The ability to accurately measure ingredients not only ensures consistent results but also allows you to confidently experiment with recipes and adapt them to your needs. The more you practice, the more comfortable you'll become, transforming fractional challenges into culinary triumphs. Remember, precision in measurement is a key to success in the kitchen. Mastering fractions empowers you to confidently navigate recipes and create delicious dishes every time.
Tips for Accurate Measurement
- Use the right measuring tools: Invest in a good set of measuring cups and spoons. Avoid using mismatched or worn-out tools.
- Level your ingredients: Use a straight edge (like a knife or spatula) to level off dry ingredients in your measuring cups. Avoid packing them down.
- Check your measurements: Double-check your measurements before adding ingredients to your recipe. It's better to catch any errors early.
- Practice makes perfect: The more you work with fractional measurements, the more comfortable you will become. Don’t be afraid to experiment and learn from your experiences.
By understanding the principles outlined here, you can confidently tackle any recipe involving fractions, enhancing your culinary skills and your baking or cooking experiences. Remember, precision is key, but don't be afraid to experiment and have fun in the kitchen!
Latest Posts
Latest Posts
-
30 Days Before October 7 2024
May 25, 2025
-
10 Over 15 As A Percentage
May 25, 2025
-
12 1 2 As An Improper Fraction
May 25, 2025
-
What Is 1 2 Of 14
May 25, 2025
-
What Is 16 Percent Of 100
May 25, 2025
Related Post
Thank you for visiting our website which covers about 3 4 Plus 3 4 Equals In Cups . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.